Volume 10
Issue 3, 1996
Economic Optimisation: An Excel Alternative to Estelles et al's GAMS Approach
- Ziggy MacDonald
- University of Leicester
Introduction
In a recent edition of CHEER
Estelles et al (1996)
presented a paper discussing an approach to teaching economic optimisation
using the GAMS (General Algebraic Modelling System) software. GAMS is a
powerful modelling language which can cope with very large programming
problems of varying types (e.g. integer, non-linear, etc.). The fact that
it is a high level language is perhaps the reason that drives me to
question its suitability as a teaching tool. Although students should be
encouraged to explore a variety of problem solving tools, thus widening
their portfolio of skills, my suspicions are aroused when the tool
requires the user to employ two applications in order to generate the
output from one application. Such is the case with solvers such as GAMS
where an input file containing the instructions for the solver has to be
created in a third party text editor. Having run the input file through
the solver an output file is generated which, of course, then has to be
viewed in a text editor.
The purpose of this response to Estelles et al is to show that not
only is a common place Windows spreadsheet such as Excel far friendlier
for students to use, it also allows greater flexibility and speed for
post-optimality analysis. The strong appeal of Excel Solver lies in its
ease of use and the enlightening nature of spreadsheet work, a point
echoed by Hillier & Lieberman (1995), who in
discussing the arrival of spreadsheets solvers such as excel, commented
that "the convenient data entry and editing features of spreadsheets also
are very helpful in constructing linear programming models" (p 131). In
addition, many students on UK campuses have a sound grounding in the basic
use of Excel as it is the industry standard spreadsheet and spreadsheet
use has been widely encouraged in economics education for years (e.g. Judge 1990, Judge 1996). Thus,
unlike with GAMS, the student does not have to become familiar with a new
syntax or procedure for declaring variables and accessing routines. The
recognition of the potential of Excel Solver is also starting to appear in
textbooks, particularly Hanna (1996), where others
have traditionally relied on LINDO as the standard instructional software
(e.g. Wilkes 1989, Winston
1995, Ravindran et al 1987).
Using Excel Solver
Optimisation in Excel is achieved via the Solver Add-In (installed in
Excel from the menu option Tools | Add_Ins and subsequently accessed from
the menu option Tools | Solver). The basic process of setting up an
optimisation problem is discussed in detail in
MacDonald (1995) but essentially it requires the user
to use cell formulae to relate the objective function and constraints to
cells that are designated as 'changing cells' i.e. the decision variables.
To illustrate this, consider the example used in Estelles et al, given in
Problem 1. This is a simple 'diet problem' in which the cost of purchase
(C) of two foods (x
1, and x
2) has to be minimised
subject to the provision of the correct daily nutrient requirement
(assumed to be only calcium, protein and vitamin A) acquired from their
consumption.
Problem 1: A Simple LP
(Note 1)
Min C = 0.6x1 + x2
|
| s.t. | 10x1 + 4x2 >= 20 | (calcium)
|
| | 5x1 + 5x2 >= 20 | (protein)
|
| | 2x1 + 6x2 >= 12 | (vitaminA)
|
| | x1,x2 >= 0 |
|
The process of entering this problem is given in Figure 1. As a slight
modification I have put the objective function coefficients in separate
cells so that these can be easily changed during post-optimality analysis.
Note also that there is no restriction on the format of setting up the
problem. For clarity I have structured the problem vertically with each
component of the model having its own row, and constraint LHS and RHS
formulas and values entered into adjacent cells. However, there is nothing
to stop the user setting up a table of constants (as the problem was
originally presented in Chiang) and structuring the problem around this
table.
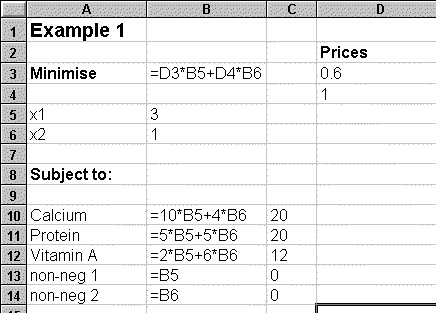
Figure 1
Having set-up the cell formulas in the spreadsheet, the user then has
to reference the problem in the Solver dialogue box (shown in Figure 2)
and simply click 'Solve'.
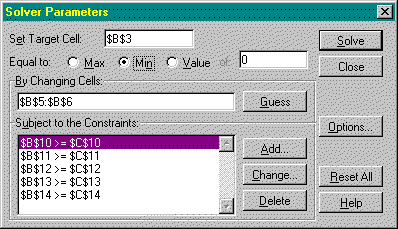
Figure 2
Unlike GAMS, where the problem solution is buried in a large output file,
on clicking 'Solve' the answer is quickly revealed in the spreadsheet
cells and an option to create an answer and sensitivity report is
provided. The answer report for this simple problem is given in Figure 3.
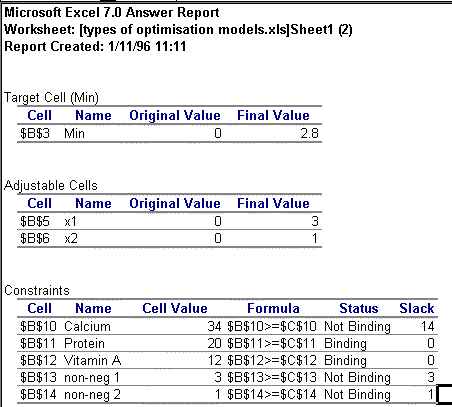
Figure 3
The answer report reveals not only information about the optimal solution
but also the status of the constraints. Should the user get an unexpected
answer, the report is also useful for debugging as the constraint formulas
are given (although it is just as simple to select the Solver and check
them in there).
Post-Optimality Analysis
One of the real advantages of Excel is the ease with which post-optimality
analysis can be executed. The relevance of the range of optimality for
objective coefficients and the meaning of shadow prices rarely appears to
filter through to students when first discussed in a lecture. Sitting in
front of Excel, however, and the subject comes to life, and this is
possibly the most significant distinguishing feature between Solver and
GAMS. The problem with GAMS as a teaching aid is that in order to
illustrate the effect of incremental changes in, say, objective
coefficients, and in particular, to illustrate the 100% rule, the user has
to go in and out of a text editor several times. In Excel the process is
smooth and instantly revealing. Consider the example illustrated above.
The answer and sensitivity reports are generated in the worksheets
adjacent to the original problem. Provided the user has selected "Assume
Linear Model" from the Option dialogue box, the sensitivity report
provides information on allowable ranges for objective function
coefficients and RHS values in addition to the usual reduced cost and
shadow price information. The sensitivity report for the problem
illustrated above is provided in Figure 4.
Figure 4
Consider changing the price of good 1 (x1) from 0.6 to 0.9. The
sensitivity report reveals that this is within the range of optimality
(i.e. below the maximum allowable increase) and so the optimal values of
x1 and x2 should remain unchanged. To test this the
student has only to change the one cell in the spreadsheet, click to solve
again and the new value for cost and the unchanged decision variables
appear instantly (x1 = 3, x2 = 1, C = 3.7). Given
this simplicity it is yet more revealing when students put the 100% rule
to test (i.e. that for a simultaneous change in objective coefficients,
provided the sum of the changes as expressed as a percentage of the
corresponding allowable increase/decrease does not exceed 100% the optimal
values of x1 and x2 should not change (Note2)). What is more, exploring the meaning of the
shadow prices given in the sensitivity report is equally as simple because
the RHS values for each constraint are given in separate cells in the
spreadsheet. A simple change to the RHS of the protein constraint (the
only binding constraint in this problem), say to a requirement of 21 units
per day, will reveal to the student, on re-solving, an increase in cost of
0.08, as predicted by the shadow price. As with the objective
coefficients, the student could then proceed to test the allowable range
for the RHS values by resolving and generating new sensitivity reports to
observe the effect on the shadow price.
Types of Optimisation
Not only is observing the effects of model re-specification a simple and
straightforward process, it is equally as simple to modify the type of
optimisation being considered. In most cases you do not have to specify
the type of optimisation you wish Excel Solver to undertake. Referring
back to the simple diet problem, it is perhaps realistic to assume that
only integer values should be used for the daily consumption of the two
foods (although, fortunately, the optimal solution is already integer).
Assuming the integer requirement was necessary, as would be the case if
the price of good one were £1 rather than 60p, all that is required
is to add two further constraints in the Solver dialogue box, shown in
Figure 5, which reference the changing cells (the decision variables) and
force them to integer.
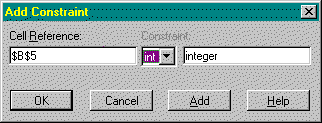
Figure 5
A particularly useful feature of Excel Solver is the option to have the
solution paused at each iteration. This is achieved from the 'Options'
button in the Solver dialogue box by checking the option 'Show
Iterations'. If we make the change to the original diet problem so that
the cost of good one is £1, then using this option the student can
see that the LP solution takes 6 iterations. Forcing the changing cells to
take integer values then requires 15 iterations to achieve the optimal
integer solution. This option can really help students appreciate the
computational requirements of integer problems. One example I use in my
third year Optimisation in Business course is a simple 5 variable, 8
constraint profit max problem that requires only 6 iterations to solve as
an LP. In the lecture I then force the integer requirement and the problem
is dramatically transformed. Remembering to un-check the 'Show Iterations'
option, the problem is solved after approximately 1000 iterations and
around 340 branches, which the students can see occur at the bottom left
of the Excel screen in the status bar. None of these facilities are
available in real-time in GAMS. Although the GAMS output does provide
detailed analysis of resource usage and iteration count, for example, this
can only be accessed after the solution is completed and the student has
read the output file into a text editor (and spend some time hunting the
rather detailed output for this information and the solution, which is
right at the end).
Finally, Excel Solver can easily accommodate non-linear or parameterised
problems as it can linear and integer problems without any special
modifications. Referring to the example in Estelles et al, given in
Problem 2, the non-linear problem is entered into Solver in exactly the
same way as a linear problem except that the option 'Assume Linear Model'
must be un-checked in the Solver Options dialogue box.
- Problem 2
- min C = 4K + 5L
- s.t. 10 K0.5L0.5 >= 1000
- K,L >= 0
Of course, further flexibility can be added to this type of problem by
putting the parameters in separate cells which can be subsequently altered
and the impact on the solution immediately observed.
Limitations
Although a fan of Excel Solver I'm not on commission and there some are
problems with the routine, particularly with respect to reduced costs.
From my experience of Solver it appears to be somewhat selective as to
when it provides reduced cost values. The theory suggests that if a
variable is not part of the basis in the solution then the reduced cost
value should indicate the amount by which the coefficient has to improve
(for a max problem) before that variable will enter the solution. If the
reduced cost value for a non-basic variable is zero then this is an
indication of the presence of alternate optima. The problem with Solver is
that invariably the reduced costs for non-basic variables are zero when
clearly there isn't an alternate optima and other packages provide values.
This is clearly a problem as such information is the bread and butter of
report writing for problems where not all variables form part of the
solution.
Concluding Remarks
Excel Solver is very accessible to students and provides a rich
environment in which to explore optimisation problems. Although GAMS can
probably handle larger problems than Excel (as it is a modelling language
and therefore specifically designed for the task), it is perhaps more
cumbersome and certainly less self-contained. The flexibility of Excel
Solver is one of its strongest attractions, particularly in respect of
exploring post-optimality changes to the original problem. Although
students have to be quite careful in defining the problem, in Excel
debugging is very straightforward and can of course assist in the learning
process. In conclusion, GAMS is clearly a sufficient medium in which to
explore optimisation problems, however, problems with reduced cost aside,
Excel Solver is better equipped to facilitate learning and will remain my
preferred solver for teaching, and invariably, a firm favourite with
students.
References
Chiang, A. C., 1984, "Fundamental Methods of
Mathematical Economics", 3rd Edition, McGraw-Hill
Estelles, T. C., Arre, M. M. & Garrido, R. S., 1996, "Economic Optimisation with GAMS", Computers in Higher Education Economic
Review, 10 (2) 2-7
Hanna, M., 1996, "Introduction to Management Science - Mastering Quantitative Analysis", South-Western
Hillier, F. & Lieberman, G., 1995, "Introduction to
Operations Research", sixth edition, McGraw-Hill
Judge, G., 1990, "Quantitative Analysis for Economics
and Business Using Lotus 1-2-3", Harvester-Wheatsheaf
Judge, G., 1996, "Student Created Spreadsheet Models
for Teaching & Learning Economics: An initial Self-Evaluation of an
Experimental Assignment", Computers in Higher Education Economic
Review, 10 (2) 16-18
MacDonald, Z., 1995, "Teaching Linear Programming using Microsoft Excel Solver", Computers in Higher Education Economic
Review, 9 (3) 7-10
Ravindran, A., Phillips, D. & Solberg, J., 1987,
"Operations Research - Principles & Practice", 2nd Edition, Wiley
Wilkes, M., 1989, "Operational Research - Analysis &
Applications", McGraw Hill
Winston, W. L., 1994, "Operations Research
-Applications & Algorithms", 3rd Edition, Duxbury (Wadworth)
Ziggy MacDonald
Department of Economics
University of Leicester
University Road
Leicester. UK
LE1 7RH
E-mail abm1@le.ac.uk
Note 1: The model given in Estelles
et al has a typo error: the RHS value of the 3rd constraint is shown as 20
whereas in Chiang's original problem (
Chiang 1984
page 652) the RHS value is 12. Estelles et al have used the correct
figure, however, in their computer solution and output.
Note 2: Although for small problems the sum can also
safely far exceed 100% without affecting the optimal solution.
