Volume 12, Issue 1, 1998
Bezier Curves for Economic Applications
- Michel Deslierres
- GEMEAP Département d'économie
Université de Moncton, Moncton, New-Brunswick,
Canada, E1A 3E9
- tel: 1 506 858-3730
- fax: 1 506 858-4508
- int: desliem@umoncton.ca
- tel: 1 506 858-3730
1. Introduction
The growing availability of powerful micro-computers with high resolution video subsystems has made possible visual, interactive presentations of economic concepts that should help students. Java has made this possibility practical. This paper presents Java classes of Bezier curves and extensions that will prove useful in constructing interactive graphs for economics.
While a Bezier curve is well behaved and easily drawn, it is difficult to find a particular point on it. The problem is that both the x and y components of the curve are cubic functions of a parameter. This is unfortunate. A simple dynamic application such as showing the opportunity cost as the student moves a point along a production possibility curve requires that points on the latter be easily identified. The paper offers solutions to this problem.
The next section contains a rapid introduction to Java. It can be skipped by those already familiar with the language. The third section exposes the mathematics of Bezier curves that are found in many drawing programmes. The most important methods of a Java class for Bezier curves are also shown. A standard algorithm for finding the root of a differentiable function is presented as a solution to the above mentioned problem.
The algorithm presented in section 3 is expensive in terms of the number of computations it requires. Another solution is to simplify the x component's parametric function. Sections 4 and 5 of the paper present two other classes of what could be called semi-Bezier curves: in section 4 the x component is a linear function of the parameter, in section 5 it is a quadratic function. In both cases, it is possible to algebraically solve for the parameter given x and then compute the y component.
The paper ends with a discussion of implementation details. In particular a method of drawing Bezier curve involving only additions is presented. All source code for these classes and example applets are available in a compressed file at the following address
http://www.umoncton.ca/desliem/java/ecbezier.zip
2. Java
Java introduced by Sun Microsystems in late 1995 is a mixture of new and old ideas. It is modern in its almost single minded adherence to the object programming concept. A Java programme is created by first compiling its source code to «byte-codes». The resulting byte-codes can then be run on any Java Virtual Machine (JVM). These are interpreters; programmes that read the compiled byte-codes and translate them into instructions for the host computer. This compilation to an intermediate code and its run-time interpretation is not unlike the UCSD p-code languages of the early 1980's.
Sun provides compilers and JVMs that run on Windows 95, Unix etc. free of charge. This means that platform independent software can be created. There are costs, of course. Java's abstract window toolkit (awt) contains only a common subset of the more important graphics user interfaces. It is difficult to control the layout of graphical elements and the appearance is likely to be slightly different on different platforms. In many cases, the most important cost is in terms of performance. By Sun's own admission, a Java programme is 10 to 20 times slower than an equivalent C, FORTRAN or Pascal programme compiled to native machine code (van Hoff (1996) p.14 and Flanagan (1997) p.8).
Many of the more important Web browsers incorporate Java virtual machines capable of interpreting special Java programmes with limited capabilities called applets. Security is ensured by preventing an applet from interacting with the file system. A browser running an applet requests only its byte-codes from the server.
It is not possible to provide a thorough introduction to Java here. There are excellent references to the language (see Flanagan (1997), Lemay (1997) and van Hoff (1996) which are only 3 among the many, many available books) including an online tutorial available from Sun (Campione (1996)). Those that are familiar with procedural programming languages such as BASIC, C, FORTRAN and Pascal may understand what follows.
Objects are collections of data and methods (object talk for procedures, subroutines, functions...) that act on the data. In procedural languages the data is often presented as an instance of a record and procedures are written to act on the record's data which is passed to them as parameters. Here is a simple Pascal program that defines a rectangle type and two procedures that can act on rectangles. The program creates an instance of a rectangle on the heap and then moves it using one of the procedures.
Program Exp;
type
Prectangle = ^Trectangle; { pointer type for rectangle records }
Trectangle = record x, y, width, height : integer end;
var
rect : Prectangle;
procedure moveRectangle(me : Prectangle; dx, dy : integer);
begin
me^.x := me^.x + dx;
me^.y := me^.y + dy;
end;
procedure rotateRectangle(me : Prectangle);
var
temp : integer;
begin
temp = me^.width;
me^.width := me^.height;
me^.height := temp;
end;
begin
new(rect); { create an instance of a Trectangle on the heap }
rect.x := 0; { initialize the record’s fields }
rect.y := 0;
rect.width := 20;
rect.height := 10;
moveRectangle(rect,10,10); {calling rectangle move procedure }
dispose(rect); {destroy the record after use}
end;
Below is the equivalent Java programme. Note the C-like syntax
which, frustratingly, includes case-sensitive identifiers.
class JavaProgramme {
Rectangle rect; // declare a Rectangle object
public static void main (Strings args[]) {
rect = new Rectangle(); // create the object on the heap
rect.move(10,20); // calling rectangle move method
} // Java’s built-in garbage
// collector takes
// care of destroying the object after
} // use.
class Rectangle {
public int x;
public int y;
public int width;
public int height;
public Rectangle() {
x = y = 0; //create a rectangle with default
width = 20; // position at (0,0) and size
height = 10; // (20, 10)
}
public void move(int dx, int dy) {
x += dx; // C type syntax for x := x + dx
y += dy; // and y = y + dy
}
public void rotate() {
int temp = width; // declaration and assignment done
// in 1 statement
width = height;
height = temp;
}
}
When the Java method move() is invoked in the main programme as rect.move(10, 20), it receives as an automatic parameter the objectrect. Hence the Java method is actually equivalent to the Pascal proceduremoveRectangle(rect, 10, 20). This example may leave the impression that the difference between object oriented languages and procedural languages is merely cosmetic. At a certain level this is true and, indeed, everything that can be accomplished with object based languages or any other language can be done in assembler and is eventually translated into machine language. This is hardly an argument proving that all languages are only superficially different from machine language. Some languages are better suited for some types of problems. Objects provide a clean solution for the following situation.
Suppose that it becomes useful to extend the definition of rectangles to add drawable rectangles. In Pascal one could define a new type of record
TdrawableRectangle = record aRect : Trectangle; fill : fillType; colour : colourType; end;
if drect were to be an instance of such a record, then a call to move the rectangle would require a "double dereferencing"
moveRectangle(drect.aRect, 10, 20);
In Java, the class DrawableRectangle defined as an extension of Rectangle
class DrawableRectangle extends Rectangle {
fillType fill;
colourType colour;
public DrawableRectangle() {
super();
fillType = EMPTY_FILL;
colour = BLACK;
}
public void rotate() {
super.rotate();
fill.rotate();
}
}
inherits Rectangle's data fields and methods. Thus if drect were an instance of DrawableRectangle, moving it is accomplished as if it were a Rectangle object :
drect.move(10, 20)
This simplification can be a boon when much use is made of inheritance. Furthermore, a class can override an inherited method if needed. In this example,rotate adds a call to rotate the rectangle's fill.
In the following sections, three classes of Bezier curves are created as sub-classes of a generic Curve class. Methods in the latter class set, get and draw the curve's end and control points. The sub-classes have methods to calculate the specific curve, to calculate averages and slopes and to draw the curve itself.
3. Bezier Curve
Bezier curves are often used in graphics programmes because they are flexible, easily controlled and can be chained smoothly. These qualities allow them to represent the typical curves of economics : production possibility curves, isoquants, demand and supply curves and so on.
A two dimensional Bezier curve is a parametric curve, which is a set of ordered couples (x,y) defined as functions of a parameter t that takes on values between 0 and 1 :
![[Equation]](bezie0.gif) (1)
(1)
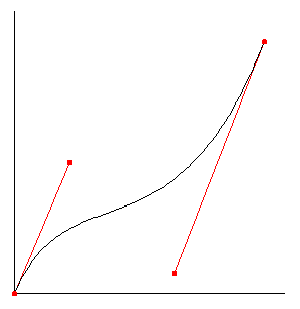
The curve's starting point, at t = 0, is (x0,y0) while its ending point, when t = 1, is (x1,y1). The other points, (cx,cy) and (dx,dy), are the control points that determine the shape of the curve. These four points define the curve entirely.
The slope of the curve at point t, m(t), is the ratio of the derivatives of the parametric functions:
![[Equation]](bezie1.gif) (2)
(2)
Since Y'(0) = 3(cy - y0), Y'(1) = 3(y1 - dy),
X'(0) = 3(cx - x0), and X'(1) = 3(x1 - dx),
the curve starts with a slope equal to (cy - y0)/(cx - x0) and ends with a slope equal to
(y1 - dy)/(x1 - dx). In other words, at the start a Bezier curve is tangent to the line segment from its starting point (x0,y0) to the first control point (cx,cy). Similarly, it ends as a tangent to the line segment from the second control point (dx,dy) to the ending point (x1,y1). The further a control point is from its corresponding end point, the more it "bends" the Bezier curve away from a straight path between the two end points. It is these characteristics which makes it easy to control the shape of the curve.
The following table provides values for typical economics curves drawn in a 300x300 grid.
| Point | Production possibility curve |
Demand curve | Supply curve | Isoquant | Cost curve | |
|---|---|---|---|---|---|---|
| starting | (x0,y0) | (0, 250) | (20, 250) | (20, 20) | (20, 250) | (0, 0) |
| ending | (x1,y1) | (250, 0) | (250, 20) | (250, 250) | (250, 20) | (250, 250) |
| 1st control | (cx,cy) | (150, 200) | (70, 115) | (70, 115) | (40, 120) | (55, 130) |
| 2nd control | (dx,dy) | (200, 150) | (145, 120) | (145, 120) | (110, 40) | (160, 20) |
In the figures, the control points are drawn and joined to their associated end point with a straight line. The Bezier curve is clearly tangent to these lines at the end points. In the supplied applets, it is possible to move any of the four points and observe the consequence on the Bezier curve.
Below are the principal Java methods of a Bezier object.
public Point calcp(double t) {
double q = 1-t;
double q2 = q*q;
double q3 = q*q2;
double t2 = t*t;
double t3 = t*t2;
return new Point(
(int) (q3*x0 + 3*t*q2*cx + 3*t2*q*dx + t3*x1),
(int) (q3*y0 + 3*t*q2*cy + 3*t2*q*dy + t3*y1) );
}
public void draw(Graphics g, int ox, int oy) {
Point p;
int lastx = ox+x0;
int lasty = oy-y0;
for (int t = 1; t <= steps; t++) {
p = calcp((double) t/steps);
g.drawLine(lastx,lasty,ox+p.x,oy-p.y);
lastx = ox+p.x;
lasty = oy-p.y;
}
}
The draw method is called with a graphics context (Graphics g) and absolute position of the logical origin (int ox, int oy). These coordinates are necessary because the origin of coordinate system used by the graphics context is the upper left corner of the image and most economic applications require a coordinate system with an origin near the bottom left corner or perhaps near the centre of the image.
Other elements must often be included in economic graphs, such as tangents or rays that illustrate marginal or average functions. Presumably, the tangent should be placed at a specific point on the curve which would normally be identified by its x component (or y component). If only one point needs to be identified, it can be obtained while drawing the curve.
public int draw(Graphics g, int ox, int oy, int x) {
Point p;
int lastx = ox+x0;
int lasty = oy-y0;
int diff = Math.abs(x0-x); // assume x = x0
int y = y0; // and y = y0 will be returned
for (int t = 1; t <= steps; t++) {
p = calcp((double) t/steps);
g.drawLine(lastx,lasty,ox+p.x,oy-p.y);
lastx = ox+p.x;
lasty = oy-p.y;
if (Math.abs(p.x - x) < diff) { // if p.x is nearer to x
diff = Math.abs(p.x - x); // prepare to return p.y
y = p.y;
}
}
return y;
}
This approach could be adapted to identify more points on the curve by using 3 arrays (or Vectors) for x, y and diff. However this would slow down the drawing method which could prove a problem in a dynamic context. It would require drawing the curve each time particular points on it are required and it would require some bookkeeping to manage the arrays' indices. What is desired is a method such as
public int calcy(int x) {
double t = some_function_of_x(x);
double q = 1-t;
double q2 = q*q;
double q3 = q*q2;
double t2 = t*t;
double t3 = t*t2;
return (int) (q3*y0 + 3*t*q2*cy + 3*t2*q*dy + t3*y1);
}
Unfortunately, defining t as "some_function_of_x" implies solving equation 2. This is not easily done. Alternatively, the root of equation 2 can be found with standard algorithms for solving equations of one variable. The methodfindt implements the Newton-Raphson algorithm (Burden (1989) pp 47-52):
private double findt(int z) {
double nt;
double t;
double t2;
double t3;
double q;
double q2;
double q3;
double ft;
double dft;
double tol;
double tol = 1.0/(double) (15*(x0+cx+dx+x1));
if (x0 <= x1)
t = (double) (z - x0) / (double) (x1 - x0);
else
t = (double) (z - x1) / (double) (x0 - x1);
for (int i=1; i<=100; i++) {
t2 = t*t;
t3 = t*t2;
q = 1-t;
q2 = q*q;
q3 = q*q2;
ft = q3*x0 + 3*t*q2*cx + 3*t2*q*dx + t3*x1 - z;
dft = 3*q2*(cx-x0) + 6*t*q*(dx-cx) + 3*t2*(x1-dx);
nt = t - (ft / dft);
if (Math.abs(nt - t) < tol) return nt;
if (nt < 0)
t = 0; // security : t must be between 0 and 1
else if (nt > 1)
t = 1; // security : t must be between 0 and 1
else
t = nt;
}
System.err.println("Bezier.java.findt failed");
return 0;
}
The method either fails or converges within 4 or 5 tries. Failure occurs when the curve is not the graph of a function, that is, when it "doubles back" on itself. The method could also be used to find t given y.
In the next two sections, modifications to the Bezier curve based on simplification of the x-component's parametric function are proposed. They allow direct computation of the parameter t given x.
4. Linear-Bezier curve
Perhaps the simplest x-component function possible is a linear function of the parameter. The resultant can be called a linear-Bezier curve :
![[Equation]](bezie2.gif) (3)
(3)
Given x, finding t is trivial: t = (x - x0)/(x1 - x0). Consequently an explicit representation of the linear-Bezier curves is possible :
{ (x, y) 2 | y=Y((x - x0)/(x1 - x0)), x0 x x1} (4)
The linear-Bezier curve has many of the properties of the Bezier curve. The slope of the curve at point t, m(t), is the ratio of the derivatives of the parametric functions :
![[Equation]](bezie3.gif) (5)
(5)
Since the slope of the curve at the start is m(0) = 3(cy - y0)/(x1 - x0), the linear-Bezier curve begins as a tangent to the line segment from its starting point (x0,y0) to ([2x0 + x1]/3, cy). Similarly, the slope at the end of the linear-Bezier curve is m(1) = 3(y1 - dy)/(x1 - x0) which is the slope of the line segment from ([x0 +2x1]/3, dy) to the ending point (x1,y1).
While not as elegant as in the case of pure Bezier curve, these tangent line segments are functions of the control points only (given the end points of the curve) and can be used to graphically guide the user wanting to set the control points.
Because X(t) is not a function of the x-components of the control points, only the y-components of the control points actually have an influence on the shape of the linear-Bezier curve. Indeed the only possible motion of the control points is vertical.
The more important methods of a Java linear-Bezier class are
public int calcy(int x) {
double t = (double) (x - x0) / (double) (x1 - x0);
double q = 1-t;
double q2 = q*q;
double q3 = q*q2;
double t2 = t*t;
double t3 = t*t2;
return (int) (q3*y0 + 3*t*q2*cy + 3*t2*q*dy + t3*y1);
}
public void draw(Graphics g, int ox, int oy) {
int y;
int lastx = ox+x0;
int lasty = oy-y0;
for (int x = x0; x <= x1; x++) {
y = oy-calcy(x);
g.drawLine(lastx,lasty,ox+x,y);
lastx = ox+x;
lasty = y;
}
}
Note that the drawing routine assumes that x0 < x1 and that x will be incremented by 1. The first constraint is not imposed in the provided code. The increment could be a variable which would allow faster drawing of the curve if required. In that case, it would be prudent to add g.drawLine(lastx,lasty,ox+x1,oy-y1); after the drawing loop to ensure that the curve is drawn to its full extent.
Most economic curves can be represented with linear-Bezier curves :
| Point | Production possibility curve |
Demand curve | Supply curve | Isoquant | Cost curve | |
|---|---|---|---|---|---|---|
| starting | (x0,y0) | (0, 250) | (20, 250) | (20, 20) | (20, 250) | (0, 0) |
| ending | (x1,y1) | (250, 0) | (250, 20) | (250, 250) | (250, 20) | (250, 250) |
| 1st control | (cx,cy) | (83, 235) | (96, 115) | (96, 115) | (96, 120) | (83, 130) |
| 2nd control | (dx,dy) | (166, 180) | (173, 120) | (173, 120) | (173, 40) | (166, 20) |
The cx and dx values of the control points have no impact on the shape of the linear-Bezier curve. However, they are required in order to place the control points in such a way that the tangents at the end points can be drawn accurately.
5. Quadratic-Bezier Curve
In some circumstances the limited flexibility of linear-Bezier curves could present a problem. Making the x parametric function a quadratic improves the situation with increased computational cost as the price.
A candidate for this function is
X(t) = (1-t)2x0 + 2t(1-t)k + t2x1 (6)
where k is a "suitably" chosen value. It is possible to solve the equation for t :
![[Equation]](bezie4.gif) (7)
(7)
The obviously unsuitable choice for k is (x0+x1)/2. Once again, the slope of the curve at t is m(t) = Y'(t)/X'(t) where
Y'(t) = 3(1-t)2(cy - y0) + 6t(1-t)(dy - cy) + 3t2(y1 - dy) (9)
X'(t) = 2(1-t)(k - xo) + 2t(x1- k) (10)
Since m(0) = 3(cy - y0)/2(k - xo), the curve starts as a tangent to the line segment from (x0, y0) to ((x0+2k)/3, cy). Similarly, m(1) = 3(y1 - dy)/ 2(x1- k) implies that the curve ends as a tangent to the line segment from ((x1+2k)/3, dy) to (x1, y1).
The x component of the control points have no impact on the quadratic-Bezier curve. Hence only vertical motion of the control points is possible as in the case for the linear-Bezier curve. However, in the latter's case, the control points were restricted to verticals at 1/3 and 2/3 of the distance between the curve's end points while in the case of the quadratic-Bezier curve, these vertical constraints can be moved by varying the value of the k parameter. There remains the requirement to maintain a fixed distance between the two verticals that is equal to 1/3 the x spread of the curve.
The quadratic-Bezier Java class is for the most part identical to the linear-Bezier class. The calcy method needs to be replaced :
public int calcy(int x) {
double t = (x0 - k) + Math.sqrt( (x0-k)*(x0-k) - (x0+x1-2*k)*(x0-x) );
t = t / (x0+x1-2*k);
double q = 1-t;
double q2 = q*q;
double q3 = q*q2;
double t2 = t*t;
double t3 = t*t2;
return (int) (q3*y0 + 3*t*q2*cy + 3*t2*q*dy + t3*y1);
}
This approach does work although it is not as tidy as the original and the linear Bezier curves. Its drawback is a result of introducing a fifth control parameter, k. Thus the cost of the increased flexibility of the curve is a somewhat more complicated process of defining a quadratic-Bezier curve: a typical economic tradeoff.
Most economic curves can be represented with linear-Bezier curves :
| Point | Production possibility curve |
Demand curve | Supply curve | Isoquant | Cost curve | |
|---|---|---|---|---|---|---|
| starting | (x0,y0) | (0, 250) | (20, 250) | (20, 20) | (20, 250) | (0, 0) |
| ending | (x1,y1) | (250, 0) | (250, 20) | (250, 250) | (250, 20) | (250, 250) |
| 1st control | (cx,cy) | (113, 235) | (73, 115) | (73, 115) | (56, 120) | (66, 130) |
| 2nd control | (dx,dy) | (196, 180) | (150, 120) | (150, 120) | (133, 40) | (150, 20) |
| fifth param | k | 170 | 100 | 100 | 75 | 100 |
Once again, the cx and dx values of the control points are required solely to in order to place the control points in such a way that the tangents at the end points can be drawn accurately.
6. Implementation
There are two important aspects to implementing Bezier curves in Java. The first has to do with the annoying screen flicker which users will experience when using the applets which accompany this article. Solutions for this is a well known inconvenience abound and will not be considered here (Lemay (1997) pp. 221-225).
The time needed to draw a curve can also be a problem. This is particularly true for applets that may be running on older micro-computers. Calculating the y component of one point on the curve using the above provided routines requires no less than 12 floating point multiplications and 3 additions plus any operations required to calculate t in some cases. That would mean 2,400 multiplications to draw a standard Bezier curve evaluated at 100 points along its length. Nested or Horner presentation of the polynomial reduces the number of multiplications by 2 and should in any case always be used as it decreases rounding error (Burden (1989) p. 18).
public int calcy(int x) {
double t = (double) (x - x0) / (double) (x1 - x0);
double q = 1-t;
return (int) ( q*q*(q*y0 + 3*t*cy) + (3*q*dy + t*y)*t*t );
}
Using the forward difference approach eliminates all multiplications needed to calculate individuals points. Rapidly, here is the rationale for the method. Let y(t) be the function to be graphed. The forward differences, as the function is evaluated at t+h, are defined as follows
D1(t) = y(t+h) - y(t) first forward difference
D2(t) = D1(t+h) - D1(t) second
forward difference
D3(t) = D2(t+h) - D2(t) third forward
difference
D4(t) = D3(t+h) - D3(t) fourth
forward difference
... and so on.
If y(t) is a polynomial of degree n, then the n-th forward difference is a constant, say Dn, and all higher forward differences can be ignored since they are equal to 0. In the case of Bezier curves, the n is 3. Working backwards, yields the following
y(t+h) = y(t) + D1(t)
D1(t+h) = D1(t) + D2(t)
D2(t+h) = D2(t) + D3.
Assuming the initial forward differences D1(0), D2(0) and D3 are known, it is possible to draw the curve point by point, starting at y(0), by applying the calculated forward differences to obtain the next point. The problem is finding the initial forward differences. Bartley (1997) transforms the Bezier curve into a standard cubic form and then calculates the forward differences. It is possible, albeit, rather complicated to calculate the initial differences for the Bezier curve (Deslierres (1997)):
public void draw(Graphics g, int ox, int oy) {
int ny;
int nx;
//Set up the step size
//
double h = 1.0 / (double) (p1x-p0x);
double h2 = h*h;
double h3 = h*h2;
double r = 1-h;
// Compute initial forward differences
//
double d3 = 6 * h3 * (y1 - y0 + 3*(cy - dy));
double d2 = d3 + 6 * h2 * (y0 + dy - 2*cy);
double d1 = r*(r*(r*x0 + 3*h*cy) + 3*h2*dy) + y1*h3 - y0;
int lastx = ox+x0;
int lasty = oy-y0;
double y = y0;
for (int x = x0+1; x <= x1; x++) {
y += d1;
d1 += d2;
d2 += d3;
ny = oy - (int) y;
nx = ox + x;
g.drawLine(lastx,lasty,nx,ny);
lastx = nx;
lasty = ny;
}
}
If a linear-Bezier curve is drawn from x0=0 to x1=199 then the forward differences approach replaces the 2,000 multiplications required with Horner representation with 16 multiplications required to compute the initial forward differences and 600 additions.
7. Conclusion
The applets supplied in ecbezier.zip illustrate the use of the three Bezier classes defined above. Furthermore, they are useful tools. In addition to illustrating typical economic relationships any of control point can be moved by dragging (clicking on the mouse button and moving the mouse button while holding the mouse button depressed). Developers can thus visually define a needed Bezier curve. It is then a simple matter to note the coordinates of each control point because they are reported in the status window when the mouse pointer is over the point.
It is hoped that this paper and the accompanying Java source will encourage development of attractive pedagogical resources on the Web for economic students.
8. Bibliography
Pierre Bezier, available online: http://www.bezier.com/Pierre.html
[No longer exists - web editor].
Bartley, Curtis, (1997), "Forward Difference Calculation of Bezier Curves", C/C++ Users Journal, November 1997, pp. 19-26.
Bourke, Paul, (1996), Bezier curves, available online at http://www.swin.edu.au/astronomy/pbourke/geometry/bezier/ .
Burden, Richard L. and J. Douglas Faires, (1989) Numerical Analysis, Fourth Edition, Boston : PWS-KENT Publishing Company.
Campione, Mary and Kathy Walrath (1996), The Java Tutorial: Object-Oriented Programming for the Internet (Java Series), Reading, Massacusetts : Addison-Wesley Publishing Company (updated and available online at http://java.sun.com/docs/books/tutorial/).
Deslierres, Michel, (1997), Calculation of Forward Differences with Mathlab, GEMEAP, Université de Moncton, Working Paper #041097.
Flanagan, David, (1997), Java in a Nutshell, Second Edition, Cambridge : O'Reilly & Associates, Inc.
Graphics, Visualization & Usability Center, (1997), Multimedia Courseware for Computer Science Education, Georgia Institute of Techonology. Available online : http://www.cc.gatech.edu/gvu/multimedia/nsfmmedia/
Lemay, Laura and Charles L. Perkins, (1997), Teach Yourself Java 1.1 in 21 Days, Second Edition, Indianapolis : Sams.net Publishing.
van Hoff, Arthur, Sami Shaio and Orca Starbuck, (1996), Hooked on Java, Reading, Massachusetts : Addison-Wesley Publishing Company.