Volume 14, Issue 1, 2000
Visualising financial concepts in the complex plane
- Michael J. Osborne
- Gulf International Bank, Bahrain (note 1)
The shortest path between two truths in the real domain passes through the complex domain.
-Jacques Hadamard (1865-1963)
Introduction
Any student of economics and finance is likely to meet complex numbers. For example, they will encounter them when studying the stability of difference equations used in business cycle analysis (see Turner (1993)).
This article shows how the complex plane can be put to a new purpose - to give a novel and visual interpretation of two important financial measures, duration and the internal rate of return. Only the most cursory of descriptions of these two concepts is given here because good, orthodox descriptions can be found in any of the many texts on finance or financial economics (for example, see Fabozzi (1996) and Cuthbertson (1996)).
The financial algebra
Consider a series of numbers, ai. Place these numbers in the particular setting of equation [1], ie, embed them in a polynomial. Equation [1] is in the form most often found in books on finance, it is the time value of money equation, while [2] is the same thing recast in the more general form found in maths books.
![]() [1]
[1]
![]() where x = (1 + r) [2]
where x = (1 + r) [2]
According to equation [1], we pay 1 out, subsequently receive a stream of returns, the ai, and get 1 back alongside the last return. Any stream of numbers can be accommodated in this structure but for the moment we focus on the fixed income bond market. Equations [3] and [3a] show the algebra of the bond pricing formula in the familiar notation of a financial calculator. Equation [3] is in the same format as [1].
![]()
![]() [3]
[3]
Equation [3] is a rearrangement of [3a] the more familiar version of the bond pricing equation.
![]()
![]() [3a]
[3a]
Setting PV = FV = 1 returns the equations [3] and [3a] to those of a par bond.
We normally think of a bond as having a stream of equal returns in which all the ai are equal but [3] shows that we can reframe the equation in the format of [1] in which the stream of numbers is constant for (n - 1) periods, but different in the final period, an. This single difference means that we have a variable stream.
The heart of this article is the more general analysis of a variable stream in which the ai can take any values. In particular we examine the way in which the ai play a part in determining the internal rate of return and duration via the complex plane.
The internal rate of return is that value of r that satisfies equations [3] or [3a] given values for all the other variables. It is a measure of the return per period on the stream of numbers, or the yield on a bond.
Duration is the first derivative of the PV (or price) with respect to r in [3a] divided by PV. It shows the interest elasticity of the price of a bond and is therefore a measure of risk. Duration has a number of valuable properties, for example, the duration of a weighted portfolio of assets is equal to the weighted average of their durations. It is useful to know when hedging risk.
Some foundations
Equation [1] is an nth degree polynomial therefore it has n roots. Usually the first real root above zero, (1 + r), is the only solution in which we are interested during any financial analysis. This number is variously interpreted as 1 plus the internal rate of return (or the real rate, the annual percentage rate, the marginal efficiency of capital, etc, depending on the interpretation of the ai.) A simple but subtle question arises at this point, a question that is not usually asked. What do the other (n - 1) roots mean?
Reference to any maths text on the subject shows that any nth degree polynomial with real coefficients will have n roots that will either be real or occur in complex, conjugate pairs (we assume none of the coefficients are complex). The fact that the complex results have an imaginary dimension means that their interpretation in a financial context is not obvious. However, the vast amount of meaning that exists for complex numbers in scientific and engineering theory is an encouragement to look deeper (see Riley, et al (1997) for a text, or Nahin (1998) for a book aimed at the lay-person).
From here on, a four period example is used to illustrate most results. This simple case is chosen because it is particularly easy to visualise the results when there are only four roots. The results are easily generalised to n periods with n roots. Where it is easy to do so, the n period case is given.
The simplest case is where the ai, are zero, ie, FV and PV are equal to 1 (there is no capital gain/loss) and all the returns are zero. Then equation [1] reduces to [4].
![]() [4]
[4]
The four roots of equation [4] are evenly dispersed around the unit circle in the complex plane (Diagram A shows the relevant Argand diagram). (note 2)
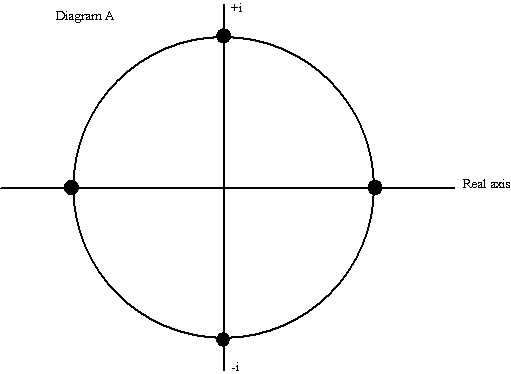
This result easily generalises to the n period case where there are n roots evenly dispersed around the unit circle with equal angles (2p/n radians or 360/n degrees) between them. The general version of [4] with n roots is known as the cyclotomic equation [4a]. If there were 100 periods there would be 100 roots distributed around the unit circle with angles of 2p/100 radians, or 3.6 degrees, between them.
xn = 1 where x = (1 + r) [4a]
For the next case assume that the ai are put into the equation and further assume, for the moment, that they are equal. The equation is that of the par bond. PV and FV are both equal to 1, and the ai are equal to the coupon. In the four period case, three (n - 1) of the roots are in exactly the same position as for the cyclotomic equation, while the fourth, the one positive real root, now takes the value (1 + r) instead of unity. The result of adding in a steady stream of returns of value a is simply to move the positive real root a distance r to the right along the real axis, ie, (1 + r) = (1 + a) = (1 + coupon). The result is depicted in diagram B.
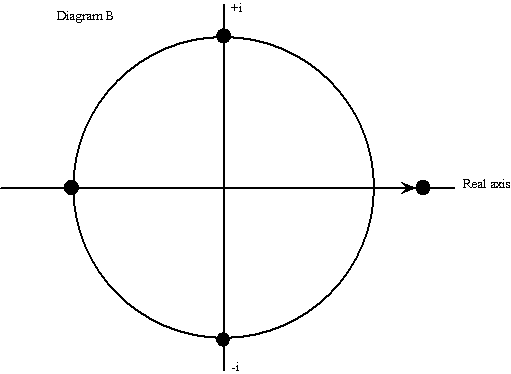
This result also generalises very easily. As the value of the ai, or the coupon, rises and falls so the real root moves to the right or the left along the real axis by equal amounts. The remaining roots, no matter how many exist, are once again distributed evenly around the unit circle.
Now allow the ai to vary in any way. For example, we can imagine the non-par bond case with all coefficients remaining constant except for the last. The last coefficient changes to reflect PV departing from the value of 1 (see equation [3]). When the ai vary, the (n - 1) roots depart from their positions on the unit circle. They become points on the ends of tendrils attached to the cyclotomic roots. These tendrils can be considered measures of dispersion from the even-flow case. In diagram C there are three such tendrils (the ti). The mathematical literature, see Erdos and Turan (1950), suggests that the roots of a polynomial with random coefficients are dispersed around specific points on the unit circle. (note 3)
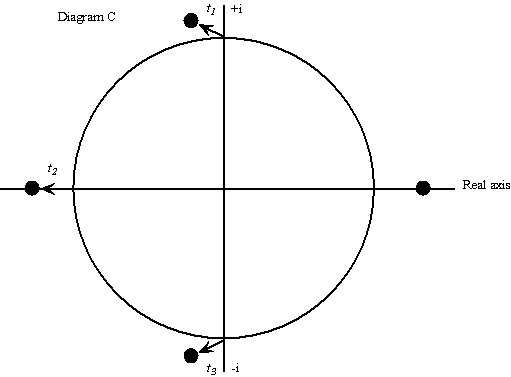
At the same time the nth root, the first positive real root, remains at it's customary position on the real axis showing the rate of return on the overall financial flow (the 'middle' of the ai). It is the output from the IRR button on a financial calculator. It is a kind of average. Indeed, below, it will be shown formally, in a surprising way, that the rate of return, r, is a particular kind of average of the ai.
Initially it is difficult to discern patterns in the positions of the roots. Professional mathematicians researching into the subject of the roots of polynomials with varying coefficients speak of its capacity to surprise. This is partly because of the difficulty of visualising what is happening in the complex plane and partly because of the complexity of the calculations. For example Farahmand (1998) says that 'random polynomials, so simple and innocent at first sight, are among the most fascinating and mysterious in mathematics. Although some of their unexpected and amusing behaviour has been known for as long as a century, yet they still reveal their secrets so that many of those both closely and indirectly involved with the subject are aroused'.
Fortunately, there exists a theorem in complex analysis that helps. It allows duration and the internal rate of return to be given simple, intuitive, geometric interpretations involving distances in the complex plane.
Cotes theorem
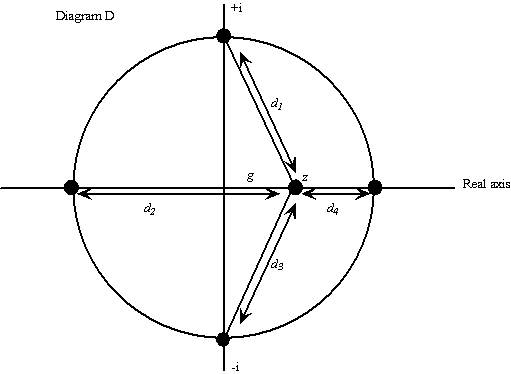
The interpretation relies on a theorem by Roger Cotes who was a mathematician at Cambridge about 300 years ago (see Nahin (1998) or Needham (1998)). Consider diagram D. Place a point, z, on the real axis inside the unit circle. The point is at a distance g from the origin. The distances of z from the cyclotomic roots are labelled di where i ranges from 1 to 4. Cotes' theorem shows the following:
![]() where the radius = R = 1 and g < R [5]
where the radius = R = 1 and g < R [5]
or
![]() where R < g [5a]
where R < g [5a]
The proof can be found in Nahin (1998) or Needham (1998) and the methodology of the proof is used in the results set out below.
Consider what happens if the point moves to the right along the real axis until it is outside the unit circle - equation [5a]. Furthermore, reinterpret the meaning of the point as the first positive real root, with the result that the distance g becomes (1 + r). The picture changes to that in diagram E and we can write equation [5a] as [5b].
d1.d2.d3.r = (1 + r)4 - 1 where r = d4 [5b]
Equation [5b] can be further modified to [5c]. It shows that the product of the distances between the first positive real root and the other (n - 1) roots in the complex plane, when divided by (1 + r)n , gives a result which is immediately recognisable. It is the sum of the discount factors. For the first time we can see a familiar financial measure in the context of the complex plane.
![]() [5c]
[5c]
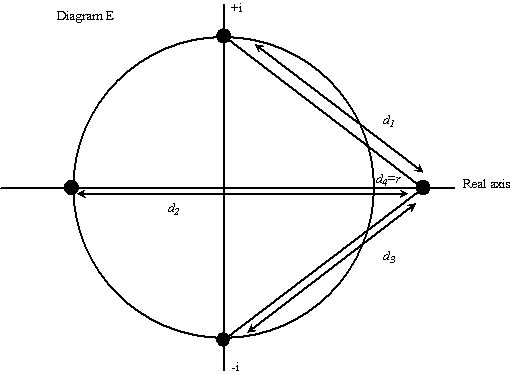
Duration for a par bond
But there is much more to it than this. The situation depicted in diagram E is equivalent to a par bond because the (n - 1) roots are the cyclotomic roots and the single real root represents the coupon (the ai in equation [1] are equal). In this special context it can be shown that the sum of the discount factors is equal to the negative of modified duration [6]. (note 4)
![]() where D is equal to modified duration. [6]
where D is equal to modified duration. [6]
This immediately gives rise to a conjecture. Is the formula in the left hand side of [6] also equal to modified duration when the ai are allowed to vary? For example, is it still true in the case of non-par bonds when the last coefficient is different from the rest, or, indeed, when we consider any stream of numbers in which each of the ai is different? The answer is yes. The proof is worth giving in full here because of its elegant simplicity and the insight it affords into the concept of duration.
The general equation for duration
Write down equation [1] n times in n rows to form a matrix, reverse the sign of each element, divide throughout by (1 + r) and call it equation [7]. In our particular example there are four rows.
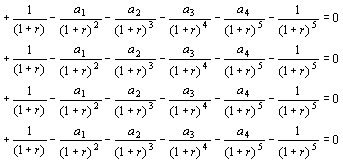
![]() [7]
[7]
The matrix is the null matrix because each row sums to zero. Partition the matrix diagonally to include the whole of the first column, the top three elements of the second column, the top two elements of the third column and the top element of the fourth column. The partition to the top left we call P1. The partition to the lower right we call P2. The elements of the matrix sum to zero, therefore P1= - P2.
Consider the two partitions in turn. First P2 because it is easier and it has the more familiar interpretation. Write down the elements of P2 in the form of an equation, slightly rearrange the final term, and it is recognisable as modified duration [8]. This could be for a par or a non-par bond, because the ai have not been specified, they can take any values.
![]() [8]
[8]
We know that P1= - P2, therefore P1 must also be equal to (the negative of) modified duration. The extra meaning of the partition P1 is not so obvious. We have to show it is equal to the left hand side of equation [6] - the product of the (n - 1) distances between the (n - 1) roots and the real nth root, divided by (1 + r)4.
We follow the line of reasoning set out in Nahin (1998). Take the universal bond pricing equation [1], reverse all the signs, multiply throughout by (1 + r)4 and set (1 + r) = z. This gives equation [9]. The notation 'z' is used because of its universal interpretation as any complex number, and here we are recognising that the various values of the root (1 + r) = z can be any number, complex as well as real.
z4 - a1z3 - a2x2 - a3z - (a4 + 1) = 0 [9]
We know that the equation [9] can be factorised to give equation [10].
z4 - a1z3 - a2z2 - a3z - (a4 + 1) = 0 = (z - z1)(z - z2)(z - z3)(z - z4) [10]
The value z is the point z in diagram D. It lies wherever we choose to set it. The zi are the roots. The absolute value of the product on the right hand side of [10] is equal to the product of the absolute values, ie,
![]() [11]
[11]
The absolute value of differences between complex numbers like (z - zi) is the distance between the two points z and zi in the plane. If we let z = z4 = (1 + r), ie, they are equal to the first positive real root, then equations [10] and [11] are equal to zero - because the very last element of both is zero. However the other three elements of the right hand side of [10] and [11] are not equal to zero. The product of these other three elements is the top element in the left hand side of [6], ie, d1d2d3 . Therefore we have to find a way to evaluate it.
Evaluating the last product is straightforward. The element (z - z4) has to be eliminated from equation [10]. To do so we divide [10] throughout by (z - z4) to give [12].
![]() [12]
[12]
Only after this division do we set z equal to z4 by replacing z4 by (1 + r) in [12], and also replace z by (1 + r). Divide the result throughout by (1 + r)4 and find the absolute value of both sides. This gives the expression [13].
![]() [13]
[13]
This is the required proof, because the left hand side of [13] is the partition P1 of the matrix, which is already known to be the negative of modified duration.
Equation [6] is now known to be true no matter what values the ai take. This can be generalised to the n period case [6a].
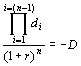 [6a]
[6a]
where the di are the (n - 1) distances in the complex plane from the chosen, positive, real, nth root to the other (n - 1) roots.
The internal rate of return
We have stated, but not proved, that the value r - the IRR - a component of the first positive real root, (1 + r), is a simple kind of average of the stream of numbers, ai.
Simple is not the usual adjective applied to the IRR because it is usually seen through the complicated algebra of the time value of money equation. Solving for r in equation [1] when n = 1 or 2 is easy. Solving for r when n = 3 or 4 is tedious. When n > 4 it is impossible to solve analytically. It has to be done using numerical methods - sophisticated guessing techniques; hence the need for a first guess in most spreadsheets and calculators, and the message 'running - running - running' when finding the IRR in the professional analyst's principal tool, the HP12C financial calculator.
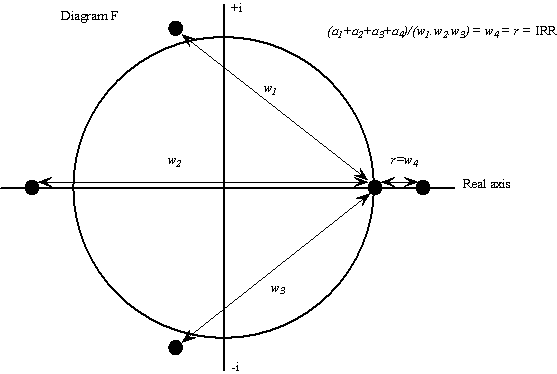
However, in the complex plane it is easy to see what it is, even if its calculation remains difficult. To see its simplicity, look at diagram F. The three rods linking the four roots in diagram E have been replaced by four rods linking all four roots to another point in the plane, the point (1,0) on the real axis. This is the same thing as setting z equal to +1 in equation [10] (instead of setting it equal to z4 as we did in the previous section). The result is equation [14] and diagram F.
![]() [14]
[14]
On the left hand side of [14] we have equation [9] with z = 1. On the right hand side we have its factorisation with z = 1. Taking absolute values on both sides means that the sum of the coefficients, the ai, is equal to the product of the lengths of the rods (the distances, n in number, from the roots to the point (1,0) in the plane). One of these distances is IRR = r = w4 = |1 - z4| therefore it is a short step to solve for it. Equation [15] shows that r is the sum of the ai divided by the (n - 1) rods (the wi with i = 1 to 3) in diagram F. Thus, the IRR is a kind of weighted average of the coefficients in the polynomial, the weights being distances in the complex plane. Like duration, the IRR has a simple interpretation in the complex plane and a new formula. Seen in this light it can also be interpreted as a measure of central tendency.
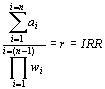 [15]
[15]
where the wi are the (n - 1) distances of the (n - 1) roots (other than the positive real root) from the point (1,0).
A summary of the results
The results can be summarised for the four period model with variable flow, ai . The four roots all lie on or around the unit circle. The real root, (1 + r), lies close to the point (1,0) because the internal rate of return, r, reflects the average magnitude of the flow - it is a measure of central tendency. The other roots lie off the unit circle if the ai are varied, or on the unit circle if they are smooth. The distances of the roots from the cyclotomic points on the unit circle (the tendrils t1, t2 and t3 in diagram C) in some way reflect the dispersion of the ai from the constant flow case. The product of the distances of the (n - 1) roots from the nth real root (d1d2d3) divided by (1 + r)4 gives modified duration.
The observations concerning the IRR and duration have been proved true no matter what the coefficients of the polynomial. Thus, duration for a bond, par or non-par, is merely a special case of a more general model. It is the special case when n coefficients in the polynomial are the same (par bond), or (n - 1) of them are the same and the nth is different (non-par bond). In the general case, the new equation for duration holds true no matter what values the ai take and no matter how many there are.
Viewing the time value of money equation through the lens of its roots in the complex plane, yields novel and elegant views of two important financial concepts.
References
Cuthbertson K. (1996) Quantitative Financial Economics, Wiley
Erdos P. & Turan P. (1950), On the distribution of roots of polynomials, Annals of Mathematics, Vol. 51, No. 1
Fabozzi F. (1996) Bond Markets, Analysis and Strategies, 3rd ed, Prentice Hall
Farahmand K. (1998) Topics in Random Polynomials, Longman, Pitman Research Notes in Mathematics
Macauley F. (1938) Some theoretical problems suggested by the movement of interest rates, bond yields, and stock prices in the US since 1856, National Bureau of Economic Research, New York
Nahin P. (1998) An Imaginary Tale: The Story of ![]() , Princeton
, Princeton
Needham T. (1998) Visual Complex Analysis, Oxford University Press
Riley K., Hobson M. and Bence S. (1997) Mathematical Methods for Physics and Engineering, Cambridge University Press
Turner P. (1993) Modern Macroeconomic Analysis, McGraw-Hill
Endnotes
3) For readers without the appropriate software to visualise the translation of the coefficients of a polynomial into roots. but who do have access to the internet, visit http://www.cecm.sfu.ca/organics/papers/odlyzko/support/polyform.html . This site contains an online calculator and graphing utility that aloows the viewer to see the roots of a polynomial in the complex plane. The limitation is that the coefficients have to take the values 0 or 1, however a 'feel' for the process can be obtained from the site.
4) It is the negative of modified duration because duration is itself a negative number. The right hand side of equation [6] must be positive to agree with the left hand side. The LHS is always positive because the top line ocnsistes of absolute values in the complex plane and the bottom line is obviously positive in most conceivable circumstances. Modified duration is so called because it is a modified version of the original concept developed by Macauley (1938).

