Osborne (2000) contains new expressions for two financial concepts from the bond markets: modified duration and the yield to maturity. The concepts are given in terms of the distances between the roots of the time value of money equation and other salient points in the complex plane. This paper offers three extensions.
First, another new expression is offered, this time a simple and elegant equation for the price of a bond.
Secondly, since its introduction by Macauley (1938), the concept of duration has suffered from several shortcomings. One of these shortcomings is the fact that the traditional formulae for duration, Macauley or modified, give estimates of the interest elasticity of the bond price that do not allow for the curvature of the link between price and the interest rate. The orthodox formula can be made more accurate by supplementing it with convexity; however, the result is still an approximation. The problem can be found illustrated in any finance text: see, for example, Fabozzi (1996).
It is shown here that the new approach to duration outlined in Osborne (2000) can be adjusted to give a formula that yields precise results for the change in the price of a bond in response to a change in the interest rate.(Note 2) This result, and the methodology surrounding it, is important because it demonstrates that the new perspective from the complex plane not only gives an alternative view of an existing concept, but also improves on it. In addition, it explains why the orthodox formula does not provide precise results, and why it cannot be adjusted to do so.
Thirdly, in order to make the theory operational in the bond markets, a question must be answered. How can the theory be adjusted to cope with bonds priced part way through a coupon period? The required level of detail in time in the bond markets is down to the individual day, and the required level of accuracy down to $1 in a million. In the context of these requirements, the new approach poses questions about computation. The questions are stated here, but not answered.
The essence of the approach is that the time value of money equation is a polynomial. A polynomial can be factorised into elements of the form (z - zi), where z can be anywhere in the plane we care to place it, and the zi are the roots of the polynomial. The mathematics of complex numbers shows that the absolute values of these elements are the distances in the complex plane between z and the zi. It follows that the time value of money, and any formula derived from it, can be seen as the product of distances in the plane. As a result, understanding the financial concepts becomes less a matter of algebra and more a matter of geometry.
The bond pricing equation (1) is a particular example of the time value of money equation with four periods. It is shown in the notation of a financial calculator. In a series of steps, the equation can be adjusted through (1a) and (1b) to the more general version, (1c). Note that the redemption or final value, fv, is set equal to 1. This assumption does not affect the results in any way; it only serves to simplify the analysis. Note also the care taken to preserve the structure of the constant term - 1 plus the coefficient. Finally, the left-hand side of (1c) can be factorised and absolute values taken, (1d). This last stage is only equal to zero if z is set
(1)
(1a)
(1b)
| z4 - a1.z3 - a2.z2 - a3.z - (a4 + 1) = 0 where z = (1 + r) | (1c) |
| |z4 - a1.z3 - a2.z2 - a3.z - (a4 + 1)| = |z - z1||z - z2||z - z3||z - z4| | (1d) |
All of the results found below, and in Osborne (2000), are obtained by allowing z in equation (1d) to approach various critical values, and manipulating the resulting output.
If, in equation (1d), z approaches 1 or, more precisely, the point (1,0) in the plane, then the following useful result holds.
 where
ri = |1 - zi| | (2) |
The absolute value of the sum of all the coefficients is equal to the product of all the interest rates.(Note 3) The absolute value of 1 minus a root is interpreted as an interest rate because each root is equal to (1 + r). In the orthodox analysis, there is only one interest rate because only one root is used. The remaining roots are discarded. In the new analysis, all roots are used explicitly. All four interest rates and roots are depicted distributed around the unit circle in Figure 1, and the distances that represent the interest rates are indicated.
If equations (1a) and (1b) are compared, and the appropriate coefficients are fed into (2), the result can be manipulated into a new bond-pricing equation, (3). The new equation says the bond price is 1 plus the sum of all the coupons divided by 1 plus the product of all the interest rates.
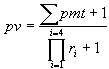(3)
This result is an elegant and memorable insight into the structure of a bond price. However, it seems to have no practical application because in order to find all the interest rates you need all the roots, and in order to find all the roots you need the price of the bond.
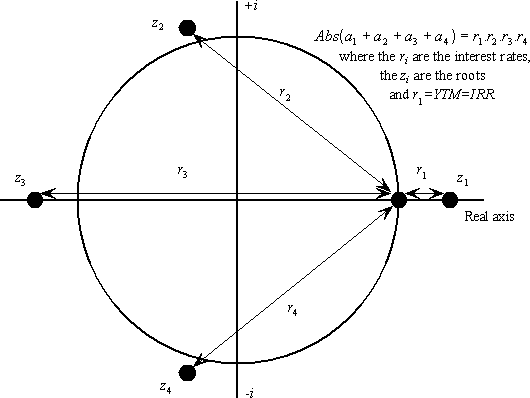
Figure 1
In Osborne (2000) an alternative and totally new expression for modified duration was derived: it is equal to the product of the distances between the positive real root and the other (n - 1) roots, divided by the positive real root to the nth power. The formula for the four-period case is equation 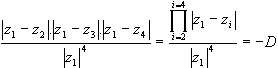(4).
(4)
where |z1| is the distance from the origin to z1=(1 + r1).
The proof of the formula is not repeated here: suffice it to say that it is obtained by allowing z in equation (1d) to converge on the principal root z1.
In contrast to the traditional equation, equation (4) can be amended to provide a version of the interest elasticity of the price of a bond that is precise.
The essence of the amendment is that only the change in the one real interest rate, r1, is allowed to affect the result. In other words, only one change of root is allowed, from z1 to a new position, call it z1*. This change affects both the top and bottom lines of (4). The next few paragraphs amplify this point.
The bottom line of equation (4) is changed very simply: replace z1 by zi*
The top line consists of the product of all the distances between the (n - 1) roots at z2, z3 and z4 and the positive real root at z1. When a new interest rate is fed into the bond-pricing equation the effect is not only on price, but also on the positions of all the other roots in the equation.(Note 4) Therefore the distances |z1 - zi| change by movement at both ends. In the new expression for duration, only the one real root z1 is allowed to move to z1* and so affect the distances. The other roots are held in place.
In other words, equation (4) must be modified slightly because in its current form both it and the traditional formula use all the roots from the same moment in time. This is incorrect. The correct formulation of the interest elasticity of the bond price uses the (n - 1) roots from the original equation before the interest rate change, and the new nth root that reflects the interest rate change. This provides an accurate bridge between the two bond prices.
The resulting formula is equation 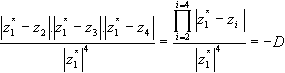(5).
(5)
where the zi are the (n - 1) roots from the starting equation and zi* is the new principal root, i.e. 1 plus the new interest rate. See the appendix for a proof.
The new expression for duration yields an insight into why the traditional formula, obtained by differentiation of the bond price, was not accurate. How many of us have puzzled over which interest rate to enter into the traditional formula for modified duration - the old one, the new one, some kind of average of the two? Clearly, differentiation of the time value of money equation with respect to the interest rate is not a simple procedure because there are multiple interest rates. Which one is being changed? It gives an interesting new slant on the famous phrase used by economists - ceteris paribus.
The new approach also answers the question about the wisdom of throwing away all the roots apart from the single real root that is traditionally calculated. All the interest rates can be used, wrapped up in their roots.
Finally, the new approach demonstrates why the orthodox formula is incapable of yielding precise results. The reason for the deficiency usually supplied in the textbooks is that duration is a straight-line approximation to a non-linear function, which is true. However, the reason supplied here is deeper than that; it is that the symbol for the interest rate contained in the orthodox equation represents simultaneously all possible interest rates. A true, ceteris paribus change cannot be made in that context. Such a change requires a formula that shows all rates explicitly.(Note 5)
The next issue is best illustrated with a numerical example. Consider a US Treasury bond with a coupon of 6% and exactly two years to run to maturity. The market rate of interest today, 3 April 2000, is 10%. The bond matures on 3 April 2002. The market convention for US T-bonds is that they pay coupons semi-annually on an actual/actual basis. If the face value is 1, then the current price is 0.929080989917. The situation is depicted in equation (6) and Figure 2.
(6)
Figure 2
Now
assume that time passes. The date is now 3 August 2000, which is
exactly two thirds of the way through the first coupon period. The
new price is 0.959797851371. The situation is no longer one of four
periods of even length, i.e. n is no longer an integer. The
number of periods is now 3
.
It is not possible to find the roots of such a polynomial.
The official method for pricing a US T-bond when a part-coupon period exists is shown in equation (7). Steiner (1998) and Fabozzi (1996) give details. The structure of the equation is that future payments are discounted back to the date of the next coupon payment (3.10.2000) and then the value on that coupon date is discounted on a fractional basis back to the present (3.8.2000). The fraction is the number of days between the valuation date and the next coupon date (t) divided by the number of days in a whole coupon period (y).
(7)
where r is the market interest rate per period.
One way forward is to crack the whole period into ten periods of two months each, the current date being time 0 and the redemption date being time 10. Coupon payments occur at times 1, 4, 7 and 10. The new approach is clearly able to handle the uneven series of payments because the ai in the original polynomials, (1b) to (1d), can take any values, including zero.(Note 6)
The result of cracking the cash flow into smaller time periods is a new polynomial of greater order than before:
(7a)
where the interest rate, r* is found from (1 + r*) = (1 + r)t/y = (1 + 0.05)1/3 .
Finding the roots of equation (7a) is easily done using one of the standard
mathematical programs like Mathcad, Mathematica, Maple or Matlab. A
precise value for duration can be calculated using only a few lines
of instructions to establish the distances between the roots. In this
example, if the market interest rate is assumed to increase by 1% on
an annual basis on 3 August 2000, then the periodic (two-month) rate
increases from 1.63963568149% to 1.80071302812% and the value of
duration,
,
is 9.23171323986. Some straightforward arithmetic using these figures
gives the change in the price of the bond as 1.48701987361%. The
actual value using the original bond pricing formula is
1.48702000641%, a difference of 0.0000001328%, or 13 cents in $1
million. One rule of thumb in the industry is that calculations like
this should yield results accurate to one hundredth of one basis
point, where a basis point is one hundredth of 1%. Thus, the required
degree of accuracy is $1 in $1 million. The answer in the example
passes this test.(Note 7)
However, the new approach does face a computational problem. The example works out beautifully because it was carefully chosen to illustrate an application of the theory using a polynomial of low degree. But consider the following extreme situation. We have a 30-year US Treasury bond and it is one day after issue. Time will need to be cracked into periods as short as one day, and the interest rate to become as small as the daily rate. The resulting polynomial is of the order of 10,950, and its coefficients are sparse. What are the limits to a computation like this? What order of polynomial can be factorised in a reasonable period of time on a good machine? And what degree of accuracy results? How far is it possible to go into the realm of practical bond calculations, given the required degree of accuracy?
In addition, if the 'period cracking' route using high-order polynomials proves to be impracticable, do any other routes exist to utilise the theoretical insight provided by the new approach? For example, if the periods are cracked into the maximum feasible number (to a day close to the actual day rather than on it) and this maximum falls short of the optimum needed for precise results, is the resulting approximation, nevertheless, a better approximation than that yielded by the orthodox calculation?
The new approach to duration is a particular example of the insight that working in the complex plane gives to any financial concept that incorporates the time value of money. The addition of the imaginary dimension is useful. It shows why the orthodox approach is inaccurate, and what can be done to correct it. In particular, it shows why differentiating the time value of money with respect to the interest rate is not straightforward. This last observation is general-it does not apply to the derivation of duration alone. Any attempt to identify a sensitivity to an interest rate change in the context of the time value of money may be subject to the problem.
However, the value of the theoretical insight is limited if it cannot be made operational. Nearly all bond traders and portfolio managers in the world have calculators built into the programs on their computers, and algorithms for duration are standard components of these calculators. The orthodox equations for duration yield only approximate results. The new approach outlined above is attractive because it suggests that precise results are possible, but only if the limits to computation have reasonable bounds. The bounds have yet to be identified. Readers with more skill than the author in these matters may be able to offer guidance or solutions.
The proof of equation (5) - the new expression for modified duration
Consider equation (1) from the text with fv set equal to 1. This is the equation that shows the price of a bond using the notation of a financial calculator simplified to the four-period model used throughout the paper.
(1)
If the interest rate changes from r to r´ then pv becomes pv´. Equation (A1) is the result.
(A1)
Convert both equations (1) and (A1) to the form of the polynomial having the particular structure described in the text - the four-period version of (1a). Call the two versions (A2) and (A3).
(A2)
(A3)
Keep these equations in mind. Now jump to equation (1d) from the text, the general version of the polynomial with n = 4 and z = (1 + r) Note that the ai on the left-hand side of (1d) correspond to the middle four parameters on the top line of (A2).
(1d)
In the text of the article it is pointed out that z can take any value. If it happens to take the value of any one of the roots, e.g., zi, then both sides of the equation are equal to zero because the first element on the right hand side is zero. In this particular case, let z converge on the new root containing the new interest rate, (1 + r´) = zi* . Substitute the left- or right-hand side of this last expression, as appropriate, into equation (1d), divide throughout by the same elements raised to the fourth power, and take absolute values on both sides. This gives 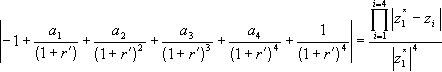(A4).
(A4)
Notice two things about (A4). First, on the right-hand side, the first of the four elements in the product on the top line is the change in the interest rate from (1 + r) to (1 + r´), i.e., |z1* - z1| = Dr . If this first element is taken outside, then the remainder is the new expression for duration, -D. Therefore, the right-hand side of (A4) is -D.Dr . (Note that D itself is intrinsically negative, therefore -D is positive.)
The second thing to notice about (A4) is the structure of the left-hand side. It is the same structure as the left-hand side of (A2) or (A3). Yet it cannot be equal to zero. This is because the ai are from equation (A2), i.e. they contain the original price, pv, while the bottom line contains the new interest rate r´ from equation (A3) rather than r. Thus, it is a mixture of the two equations. It is the old parameters being evaluated at the new interest rate. Whatever this value is, it is not zero, therefore we set it equal to X.
or
Subtract X from both sides and divide throughout by (1 + X).
Compare the coefficients in this last result with those of equation (A3). It is clear that pv´ = pv(1 + X). This means that X, the left-hand side of (A4), is the change in the price of the bond relative to its original price, i.e.
.
Put together the results from both sides of (A4) to give equation (5) in the text.
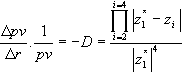 or  | (5) |
1 Mike Osborne is VP and Human Resource Development Manager for Gulf International Bank (GIB) in Bahrain. The views expressed in this article are the author's and not necessarily those of the bank. Thanks for advice go to Eggert Peterson of the University of Bahrain and colleagues at Gulf International Bank, especially Nabil Abdul Aal. The author may be contacted on email at mosborne@batelco.com.bh or mike.osborne@gibbah.com
2 The word 'precise' is used rather than 'exact'. This is because the new formula uses the roots of a polynomial as inputs. Except in special cases, there are no closed-form solutions for polynomials of order greater than four; numerical methods have to be used. Therefore, despite the fact that the formula has the appearance of a closed-form solution, it relies on numerical methods. However, the root-finding methods employed in most mathematical programs can give high levels of precision, usually greater than that needed by most financial problems, though the latter part of this paper does raise a question about the issue.
3 In Osborne (2000) the notation for these distances is wi. In this article the notation used is the more consistent ri in order to indicate that they are 'interest rates'.
4 The entry for the 'root dragging theorem' in the Encyclopedia of Mathematics (Weisstein 1998) reads: 'If any of the roots of a polynomial are increased then all of the critical points increase.'
5 It follows that any financial equation incorporating the time value of money that is differentiated to obtain the interest sensitivity is subject to the same problem. One obvious example is the interest sensitivity of the value of a portfolio of fixed rate loans in the balance sheet of a financial institution.
6 The method can be extended to find the duration of a portfolio of bonds. The orthodox approach is to calculate the duration for each bond and then find the weighted average of the durations. The new method means that the cash flows of bonds in a portfolio can be summed vertically to produce a composite bond with an uneven cash flow and irregular time periods. The lowest common denominator of time can be imposed to produce a new, higher-order polynomial with varied coefficients and integer powers. One single calculation for duration can then be made.
7 The actual bond prices, and the actual changes, were calculated to the maximum possible 11 places using the bond-pricing functions built into the HP19B financial calculator. The calculations of duration from the distances in the complex plane, and the predicted bond price change, were made using Mathcad with the precision set to 11 decimal places.
Fabozzi, F. (1996) Bond Markets, Analysis and Strategies, (3rd edn), New York: Prentice Hall.
Macauley, F. (1938) Some Theoretical Problems Suggested by the Movement of Interest Rates, Bond Yields and Stock Prices in the US since 1856, New York: National Bureau of Economic Research
Osborne, M. J. (2000) "Visualising financial concepts in the complex plane", CHEER, Vol. 14, No. 1, pp. 4-8
Steiner, R. (1998) Mastering Financial Calculations, London: FT Pitman.
Weisstein, E. W. (1998) CRC Concise Encyclopedia of Mathematics, London: Chapman & Hall/CRC.