The design and management of call centres is a task that gets more and more relevant as the use and importance of these systems increases. We have developed an Excel add-in, named SimuCall, which will help us to simulate the behaviour of this kind of service (centres as a single-queue multi-server system with some peculiarities). SimuCall handles a quick control of the parameters of a waiting system, searching its optimisation according to specific goals fixed by the call centre managers. In this paper, we have applied SimuCall to a real call centre in order to improve its efficiency. Our goals of optimising workforce and searching service efficiency have been fulfilled in a satisfactory way using this add-in. Furthermore, SimuCall is capable of providing a great quantity of information, at both aggregated and individual levels, through a variety of data and graphic reports.
It is said that more than 70% of business transactions take place over the telephone. Therefore, the presence of a call centre in the economic life of our society is indispensable in supporting business. Likewise, the appropriate design and management of this kind of service centre is essential. Modelling a call centre is a challenging task, but it is also a very topical issue. There are plenty of companies and banks that show their corporate image by means of a call centre. The virtual relationship between companies and customers is sometimes softened by the friendly voice heard on a phone. Therefore, call centre management is a very specific mission that is indispensable for the appropriate development of the company that uses the centre. But what is a call centre? Mehrotra (1997) defined a call centre as ‘any group whose principal business is talking on the telephone to customers or prospects’. This group could be situated in a single place, in a multiple position or distributed with agents in individual offices. Usually, agents in a call centre share a common set of computers and resources.
Another definition is found on the web page designed by the Call Centre News Service: ‘A call centre is traditionally defined as a physical location where calls are placed, or received, in high volume for the purpose of sales, marketing, customer service, telemarketing, technical support or other specialized business activity.’ A call centre is also sometimes described as a place for doing business by phone that combines a centralised database with an automatic call distribution system. However, it is necessary to take into account other roles of these kinds of centre, such as:
Thus the traditional role depicted in the early call centres of the 1970s has substantially changed. Nowadays, call centres are generally set up as large rooms, with workstations that include a computer, a telephone set (or headset) hooked into a large telecom switch, and one or more supervisor stations. It may stand by itself or be linked with other centres. It may also be linked to a corporate data network, including mainframes, microcomputers and LANs. Increasingly, the voice and data pathways into the centre are linked through a set of new technologies called CTI, or computer–telephony integration.
Typical companies that have implemented a call centre to administer their customer relationship management are: airline reservation centres, catalogue ordering companies, consumer-oriented problem solvers, and software customer support services. Until the early 1990s, only the largest centres could afford the investment in technology that allowed them to handle huge volumes. More recently, with the development of LAN-based switches, internet-based transaction processing, client/server software systems and open phone systems, any call centre can have an advanced call handling and customer management system, even down to ten agents or fewer.
Worldwide the call centre business is huge, omnipresent and growing fast. The first problem to face in call centre management is their size. Managers and administrators want more and more enormous centres in order to reach decreasing returns to scale. Nevertheless, the bigger the call centre, the more difficult it is to manage. Similarly, gigantic centres need optimisation more intensively than small ones. The number of call centres throughout the world is increasing because they are completely immersed in the global economy. However, the rate of growth in the number of call centres is slowing, from 4% in 1999 to an estimated 0.8% in 2003, attributed to both maturation and consolidation within the call centre industry.
We are going to highlight the importance of call centres in the current global economy, considering some statistical data that are collected on the Call Centre News Service web page. At a rough estimate, the number of call centres in North America ranges from 50,000 to as high as 200,000. The reality is probably somewhere around 100,000, depending on the definition of a call centre according to its size. It is thought that the number of call centres in Europe will grow from 12,750 in 1999 to 28,289 in 2006. Europe’s call centre market is around $9 billion. Great Britain, France, Germany and Holland together account for 80% of call centre sales revenues within the 15-member EU. During the 5-year period from 1999 through 2003, sales of call centre systems among the aforementioned countries totalled more than 1.8 million seats, over $3.6 billion in base revenues and over $9 billion in gross revenues. On the other hand, the average cost of handling a call in a telephony-based centre ranges from $50 to $74, and the average cost falls by 43% in a web-based call centre.
The experience of founding and running a call centre has been accumulated for years since the early 1970s when the first call centres were established. This know-how has been compiled in Bodin and Dawson (2002) and Dawson (2001). The first descriptive feature of a call centre is the flow direction of the customers’ calls, or who takes the initiative in the calling process. This feature classifies the call centres into inbound and outbound centres. Literally, an inbound centre is one that handles calls coming in from outside, most often through toll-free numbers. These calls are primarily service and support calls, and inbound sales. An outbound centre is one that does mainly outgoing telemarketing. Inbound is the biggest component of call centre traffic these days, although, perversely, outbound represents the area of largest projected growth in the next few years. In truth, the majority of centres contain some element of both inbound and outbound traffic.
The appropriate monitoring of a call centre is performed by the manager. Her/his role consists of ensuring the continued daily operation of the centre: that is, setting service standards for the centre (how many calls are answered, on average, or how many contacts per hour outbound agents are required to make). The manager is responsible for solving daily problems, arranging to have the optimum number of agents in the right number of seats, and making sure that the centre operates adequately, technologically speaking. Another essential responsibility of the manager is the improvement of service quality for customers. Customer relationship management is the main task of manager. Nevertheless, she/he must be ready to face any kinds of problem arising in the call centre.
Call centres are also becoming increasingly complicated to run. This peculiarity has a significant impact on the optimisation of customer management. When the first call centres were established in the early 1970s, the call management was performed using a very simple queuing mathematical model: a standard line on a FIFO basis, because the customer demanded a standard product for a standard use in a standard price. This situation was based on the uniformity of customers’ demand. Nowadays the scenario is much more complex: the customer, from the point of view of the company, is different depending on her/his preferences, purchase history and advertising reference, and the bundle of products that she/he has obtained. Lastly, the call centres profile a close relationship with clients, being the carriers of the footprint of quality for most customers. As a result, sales and service in a call centre are usually connected in a decisive way, forming a strategic advantage.
As a final point, we highlight that the description of the term ‘call centre’ is continuously changing. Now, it is possible to find call centres that answer emails, engage in live internet chat sessions with customers and sometimes even transmit live video. Therefore experts are looking for a broader definition of what a call centre is.
The use of spreadsheets in OR/MS and, particularly, in simulation is well known in the managerial community. They have been successfully tested in diverse scenarios. Gass et al. (2000) and Grossman (1999) provide outstanding examples of the excellent qualities of spreadsheets in the decision-making arena. Some other authors have even developed efficient Excel/VBA-based programs for simulating queuing models (Albright, 2001; Gross and Harris, 1998). This paper follows that direction and shows how it is possible to use the analytical and graphic capabilities of Excel to construct a VBA program, SimuCall, that gives detailed information about call centre behaviour.
In the optimisation field, by means of simulation, we highlight the work of Brigandi et al. (1994), which developed a call-processing simulator for inbound call centres at AT&T. Other current application for driving a strategic change to the management of this type of centre is explained in Saltzman and Mehrotra (2001).
The article by Aksin and Harker (2001) contains some ideas about the specific and complete organisation of call centres, using queuing theory in a more theoretical ambit. On the other hand, van Dijk (2000) develops other ideas about the use of simulation in the queuing arena that deserve detailed analysis as regards the appropriate performance of call centre simulation. The outlook of these articles is essential for comprehending the appropriate development of telephone call centres.
Finally, it is necessary to pinpoint the goal of using simulation in the description of call centres. And so, it is possible to begin in earnest the debate about call centres: cost control versus service improvement. We delve into the core of a service system because we undoubtedly want to optimise the performance of some of its outputs, albeit that we do not know which ones. Somehow, the dilemma previously depicted is classical in any service system. Nevertheless, SimuCall does not presuppose the goals or aims of the decision maker. It is a queuing simulator adapted to a call centres scenario, whereby the manager of the system could change her/his goals in different situations according to the wherewithal of the centre.
We chose simulation for designing the structure of call centres because it was the easiest way to monitor the changing scenarios of these service centres. Otherwise, it might have been very difficult to model waiting centres using exact mathematical representations. The choice of a spreadsheet as the basis for developing the call centre simulator was due to its flexibility and the spread of its usage in the managerial community. On the other hand, the employment of add-ins in management is very popular and some add-ins could be rounded off each other for improving control of the call centre. Simulation add-ins can be found everywhere. We can cite amongst many: @Risk, Crystal Ball, Exotic Options Simulations, Exotic @nalist and Insight (Thiriez, 2001). Our purpose was to customise a simulator for specific use in a call centre. It is clear that the previous add-ins could be employed for simulating any service system, call centres included.
Simulation was chosen because it is extremely difficult to implement other mathematical models for describing client flow with a computer tool. Thus, we have designed an Excel add-in in VBA code for the specific simulation of queues in call centres. But what is the reason for designing particular simulators for call centres? How is a call centre different from other queuing structures? The answer is the phone line. The queue dynamics are different in a call centre than in a physical line, such as a set of checkout points in a superstore. The queue management in a call centre is much lither than in a traditional line: it is possible to change the queue discipline, to distinguish among different kinds of customer, to control the number of customers in line, etc. without the clients in the holding line realising that something has been altered. On the other hand, the dynamics of clients are also diverse: it is important to gauge the proportion of clients that balk the line or renege in the queue. We pay special attention to those situations of balking and reneging because they represent an excellent measure of the service quality that the call centre gives to the customers. The blueprint of a simulator, having call centre optimisation as the main goal, is essential for the correct development of this kind of queue.
Let us begin by explaining how SimuCall works. SimuCall is a single-phase multi-server queuing simulator developed by the authors in order to find appropriate values for the parameters of a call centre: in other words, SimuCall is a parameter tuner for queues in a call centre. SimuCall has been coded in Visual Basic, keeping in mind its implementation in Excel 2000 or 2002 as an add-in. Once the code is working in Excel, we can see nine worksheets, which we can comment upon by order of appearance as follows:
It is easy to understand that the next task – after the introduction of several values in the input cells – is to adjust the parameters in order to reach a good performance of the simulator. This is the most artistic undertaking for the call centre modeller.
Now, we are going to describe the general procedure for running the SimuCall simulator. As mentioned above, the inputs sheet allows the user to submit the ruling parameters for call centre queues. First of all, some initial parameters are needed: time units and the inter-arrival times distribution. SimuCall assumes that the inter-arrival times can be split up into four intervals whose range can be modelled by the user. The range and the parameters can be different for each interval, but the type of probability distribution must be the same for those intervals.
In other cells, the service time distribution, the abandonment time distribution, the number of servers and the maximum number of clients in the queue must be provided. The cells that need these inputs are coloured in green. In some cells, it is necessary to click on them in order to choose between several options. In others, a click leads to a short explanation about the parameter to submit. The simulation can be controlled by the user, bounding the simulation time and the iterations number to run in the last cells of the input sheet. Once all the parameters and distributions have been specified, the simulation is begun by clicking the starting button.
The simulation outputs sheet writes, iteration after iteration, the complete values for the simulation process: arrivals, abandonment estimation, clients rejected, clients served, etc., adding up total quantities for each defined variable. Similarly, the average and maximum values are also computed. The final report sheet shows the main estimations about the line descriptions, as depicted in Figure 2.
The remaining five sheets are devoted to drawing summarised data on convenient graphs. This will facilitate the comprehension of the simulation upshots by the end user (generally speaking, the call centre manager).
We are going to justify the necessity of SimuCall’s development and use as an interesting alternative to the use of some well-known simulators for Excel, such as @Risk, Crystal Ball and Insight. It is clear that a specific simulator can describe a queuing system better than a general purpose one. But this explanation is not the raison d’être for the construction of this new add-in. We can summarise the motives for producing a simulator focused on call centres in the following points:
The Universitat Oberta de Catalunya (UOC) is a completely virtual university having its head offices in Barcelona (Spain) and teaching over the internet in Spain and Latin America. It is one of the pioneering universities in the e-learning world. It was founded in 1995 with 200 students and registered more than 20,000 students in 2002. The UOC has integrated the information and communication technologies tools in the syllabus for each university subject. Taking into account the distance teaching of this university based on the internet, it is evident that students, users and people in general need a direct contact to the UOC. This contact takes the form of several inbound call centres. For this paper, we have selected one of the several call centres that the UOC offers to its students. From now on, we will call the selected call centre ‘UOC call centre’ or simply ‘UOC CC’. This particular inbound call centre has been working properly for several semesters. It receives phone calls in a schedule ranging from Monday to Friday between 8.45 a.m. and 7.45 p.m. (11 hours per day or 55 hours perweek). In accordance with the general description of a call centre, the UOC CC is an inbound communication system having a standard line on an FIFO discipline. The purpose of the people who call the UOC CC is to obtain information about a wide range of issues related to real practice in learning and teaching over the internet at the UOC. Commercially speaking, the UOC CC is the welcoming voice that helps to solve problems or that explains the inner operations of this online university. Therefore, the appropriate working of the call centre is essential for the corporate image of the UOC.
The UOC CC fulfils a set of characteristics that make it interesting for evaluation using SimuCall: we have a complete database of observations about its daily working (number of inbound calls, number of answered calls, number of reneged calls, etc.); the number of arrival calls in this service centre is quite stable; servers are well trained and experienced in dealing correctly with students; and finally, it is a small call centre, whereupon its management is not extraordinarily difficult.
Our final intention is to analyse the selected call centre system using the discrete event simulation algorithms integrated in SimuCall. Nevertheless, before performing the analysis, we need to model the service system. To begin with, we should pinpoint the main goals targeted at this service centre. These goals could be described as follows, according to their level of relevance:
Therefore, taking into account these goals, we are not specially interested in estimating total service costs (we will leave that problem to the managers). As far as we are concerned, we will consider it worth using one or two extra agents if this policy results in a significant improvement in service quality (this idea is also enforced by the fact that when an agent is not attending a call, he or she can still be answering student emails or helping with the Frequent Asked Questions database). Efficiency, quality and promptness in service are the fundamental tenets in the management of this call centre.
Once we know both the call centre properties and our goals, we can start to build up a mathematical model for this system. Our starting point is the system database for the trimester January–March 2002 (Faulin and Juan, 2002). This database contains information about the call centre dynamics (arrival time for each call, service times, abandonment times, etc.). Since it is not easy to obtain all these data for every day in the trimester (basically due to technical reasons), we have randomly selected a sample of 10 working days for each of the 3 months. The sampled manipulation. We can describe the following phases for the modelling process.
After we have gathered the arrival times from the database, it is natural to check the hypothesis that the average number of calls arriving in the system is approximately constant for the 3 months (i.e. we want to know if it makes sense to assume that the number of arrivals remains stable enough from January to March). In order to check this hypothesis, we used the statistical package Minitab to carry out the associated ANOVA test, as can be seen in Figure 3.
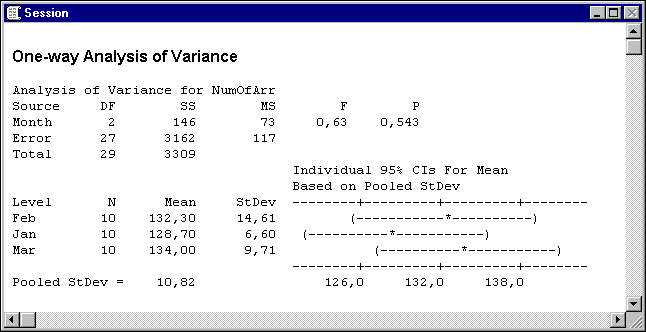
The ANOVA test points out a value of 0.63 for the F statistic, with an associated p-value of 0.543. Therefore, it seems reasonable to assume a stable behaviour in the monthly average number of calls arriving at the centre. Before accepting this conclusion as valid, we also have to check for the assumptions of ANOVA:
We are also interested in finding out if the arrival rate keeps constant all day long or if it takes significantly different values depending on the hour of the day. Since we know arrival times for each day, we can use Excel to calculate the daily number of arrivals per 15-minute period from 8.45 a.m. to 7.45 p.m. After that, we can calculate averages of these numbers (by period) and create the histogram shown in Figure 4.
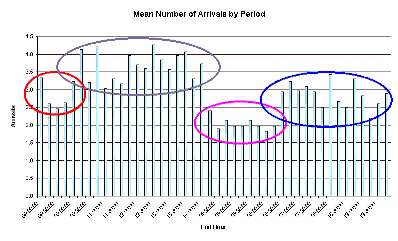
The geometrical structure of the arrival rate in Figure 4 suggests that this rate varies according to the hour of the day. Fortunately, SimuCall allows for the possibility of modelling the call inputs in different time intervals. As suggested in the histogram, it is possible to split the arrival range into four intervals whose borders can be profiled by the modeller. According to the number of calls depicted in Figure 4, we can define the following time intervals or time strips for the arrivals to the call centre:
Therefore, we seize on the SimuCall structure to find out the most appropriate probability distribution for each time strip.
Knowing the times for customer calls, the inter-arrival times can easily be calculated in an Excel worksheet as shown in Figure 5 (each inter-arrival time can be calculated as the difference between two consecutive arrival times). Later, we will have to fit inter-arrival times to a theoretical probability distribution.
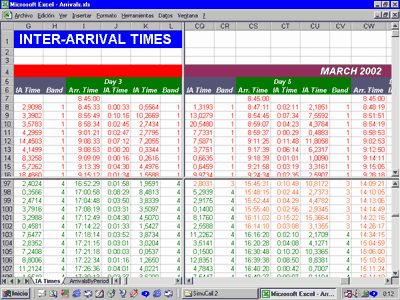
Again, we can use Minitab to fit the data to an appropriate probability distribution in several scenarios. We chose the Anderson–Darling test (Stephens, 1974) for verifying the origin population of the data. We tried to fit the data with all of the following theoretical distributions: gamma, Weibull, exponential, normal and lognormal. First, we considered the data as a whole for each day; afterwards, we split the days up into the four time strips as explained previously. After an intensive mathematical analysis, we can conclude that the best distribution for fitting the inter-arrival data is a Weibull distribution having different parameters in each time strip. This information is summarised in Table 1. Exponential distribution could be also used for fitting these data because the Anderson–Darling test reaps good outcomes for that distribution; however, the Weibull distribution is the best option according to the same test.
This task is the other side of the same coin in the simulation process. We need a probabilistic representation for the service tasks and another for the abandoning process (in a call centre system, we can consider a balking customer as a reneging one with a time of abandonment close to zero). In this case, the UOC CC managers gave us a sample of 230 observations for service times in the period January–March 2002, and another sample of 115 observations for abandonment times in the same period. Using these two samples and the Minitab package, we have been able to infer the following assertion: in this case, service times can be modelled by an exponential distribution while abandonment times need a Weibull distribution. This conclusion has been reached according to the values of the Anderson–Darling test. In both cases, neither the distribution nor the parameters depend on the time strips that have been defined for the arrival times. The convenient values for the parameters of the service times distribution and the abandonment times distribution are depicted in Table 2.
This parameter tuning has been revealed as essential to the description of the dynamics of the call centre. Once we have defined all the input parameters of this system, we can start the discrete event simulation.
| Weibull distributions | Inter-arrival times as a whole | First strip (08:45–10:00) | Second strip (10:00–14:00) | Third strip (14:00–16:15) | Fourth strip (16:15–19:45) |
| Shape parameter (α) | 0.97676 | 0.95670 | 1.02016 | 1.04259 | 0.97254 |
| Scale parameter (θ) | 4.93027 | 4.8677 |
4.0986 |
7.2460 | 5.2925 |
| Mean | 4.9810 | 4.9680 | 4.0650 | 7.1258 | 5.3574 |
| Weibull distributions | Service time (exponential) | Abandonment time |
| Shape parameter (α) | 1 | 0.6495 |
| Scale parameter (θ) | 9.4438 | 0.2728 |
| Mean | 9.4438 | 0.3731 |
The model for the UOC CC has already tuned in SimuCall. The main concerns of the system managers are associated with finding the optimum workforce size. This is a typical analysis in queuing optimisation. Therefore, we defined several scenarios to analyse. These scenarios varied in the number of servers hired by the UOC CC. The call centre managers estimated that if some of these servers are idle (they are not serving clients), they could carry out other similar tasks like answering emails, paperwork management and helping with the FAQs database. At this point, it is convenient to keep in mind that the treatment of clients in the call centre must be outstanding, according to UOC policy, meaning that the number of lost calls (balking and reneging clients) should not be greater than 5% of the total calls. As explained above, the potential scenarios to consider in the UOC CC are related to the number of servers to assign. Based on management criteria, it is clear that a minimum of two servers are required. One server working alone could not attend properly to the clients. Let us consider scenarios varying the number of servers in the range between 2 and 5. More servers would not achieve much more efficiency in call centre management and the associated cost would be excessive. Performing the simulation using SimuCall, we get the upshots depicted in Table 3. For each scenario, we obtain numeric and graphic reports. Figure 2 shows one of these numeric reports: the scenario associated with n = 5 servers.
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |
| Number of servers | 2 | 3 | 4 | 5 |
| Maximum time in queue for any customer (minutes) | 3.8 | 4.2 | 4.45 | 3.55 |
| Average time in queue for any customer (seconds) | 8 | 4 | 2 | 1 |
| Average number of customers served | 82 | 108 | 122 | 133 |
| Average number of lost clients | 38.3% | 19.4% | 9.0% | 2.9% |
| Idle time per server | 40.5% | 48.3% | 55.7% | 62.7% |
Taking into account these simulation outcomes, and the policy of less than 5% lost calls, we recommended a workforce size of 5 servers for the UOC CC. Our advice was based on the following findings:
For these reasons the optimal decision is to employ 5 servers. Figure 6 shows two of the relevant variables for each scenario.
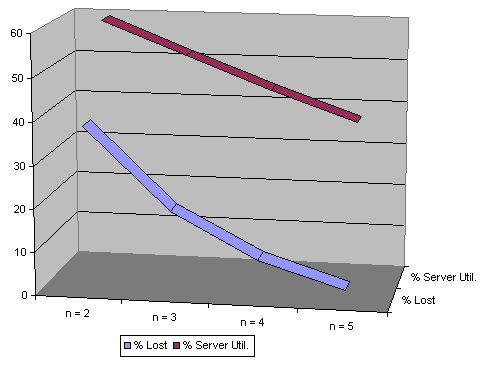
| n=2 | n=3 | n=4 | n=5 | |
|---|---|---|---|---|
| % Lost | 38.3 | 19.4 | 9 | 2.9 |
| % Server Util. | 59.5 | 51.7 | 44.3 | 37.3 |
When we discussed this result with the UOC CC managers and workers, they agreed that our simulation output was quite consistent with their own experience (which helped to validate our model). Furthermore, they realised that the policy we proposed was very similar to the one currently implemented in the call centre. Nevertheless, the complete 3-month analysis of the UOC CC helped the managers to assign specific tasks to the servers when they were idle. Implementation of our recommendations involved a one-server increment in the number of servers in the call centre, along with new ideas about training servers for the call centre.
We chose simulation for designing the structure of call centres because of the intrinsic dynamics of this kind of centre. SimuCall helps call centres to take the right decisions in the workforce design arena. Perhaps the main virtue of this add-in is its adaptability to any new situation involving queuing problems in call centres. Concerning the UOC CC, we have been able to model the waiting line of this system, supplying valuable advice about the workforce size. Other kinds of advice could be supplied, such as maximum length of queue permitted, design of workforce size per time strip, and specialisation of servers according to the necessities of the customers. In fact, the UOC CC managers have asked to us for a longer and deeper analysis of their system, so that they can consider other workforce details, such as the possibility of hiring some part-time servers. Following this line, we are currently working on a new release of SimuCall that will surely improve many aspects of the current version.
The authors are grateful for the help supplied by the managers of the UOC CC in applying the first release of the SimuCall add-in. Similarly, we would not have written this paper without the overwhelming number of phone calls of students and potential students of the Universitat Oberta de Catalunya. We appreciate this indirect help. We are also grateful to the UOC CC managers for recognising the potential of the students to influence operations improvement in organisations.
Aksin, Z. and Harker, P. (2001) ‘Modeling a phone centre: analysis of a multichannel, multiresource processor shared loss system’, Management Science, 47(2), February, pp. 324–36.
Albright, S. C. (2001) VBA for Modelers: Developing Decision Support Systems with Microsoft Excel, New York: Duxbury.
Bodin, M. and Dawson, K. (2002) The Call Centre Dictionary (3rd edn), Gilroy, CA: CMP Books.
Brigandi, A. J., Dargon, D. R., Sheehan, M. J. and Spencer, T. (1994) ‘AT&T Call Processing Simulator (CAPS) operational design for inbound call centres’, Interfaces, 24(1), January–February, pp. 6–28.
Dawson, K. (2001) The Call Centre Handbook: The Complete Guide to Starting, Running, and Improving your Call Centre (3rd edn), Gilroy, CA: CMP Books.
Faulin, J. and Juan, A. (2002) ‘Designing a simulation add-in for describing the strategic change in a call centre’, Proceedings of the International Conference on Modeling and Simulation in Technical and Social Sciences, Girona (Spain), June, available online at http://www.uoc.edu/ .
Gass, S. I., Hirshfeld, D. S. and Wasil, E. A. (2000) ‘Model world: the spreadsheeting of OR/MS’, Interfaces, 30(5), September–October, pp. 72–81.
Gross, D. and Harris, C. (1998) Fundamentals of Queueing Theory, Pacific Grove. CA: John Wiley & Sons.
Grossman, T. A. (1999) ‘Teacher’s forum: spreadsheet modeling and simulation improves understanding of queues’, Interfaces, 29(3), May–June, pp. 88–103.
Mehrotra, V. (1997) ‘Ringing up big business’, OR/MS Today, 24(4), August, pp. 18–24.
Saltzman, R. M. and Mehrotra, V. (2001) ‘A call centre uses simulation to drive strategic change’, Interfaces, 31(3), part 1 of 2, May–June, pp. 87–101.
Stephens, M. A. (1974) ‘EDF statistics for goodness of fit and some comparisons’, Journal of the American Statistical Association, 69, pp. 730–7.
Thiriez, H. (2001) ‘Improved OR education through the use of spreadsheet models’, European Journal of Operational Research, 35, pp. 461–76.
Van Dijk, N. (2000) ‘On hybrid combination of queueing and simulation’ in Proceedings of the 2000 Winter and Simulation Conference, Orlando (Florida), ed. by J. A. Joines, R. R. Barton, K. Kang and P. A. Fishwick, pp. 147–50.
Javier Faulin
Department of Statistics and Operations Research
Los Tejos Building, second floor
Campus Arrosadia
Public University of Navarra
31006 Pamplona
Navarra
Spain
Tel: 34-948169211
Fax: 34-948169204
Email: javier.faulin@unavarra.es
Angel A. Juan
Department of Applied Mathematics I
Avda. Doctor Marañón, 44–50
Polytechnique University of Catalonia (UPC)
08028 Barcelona
Spain
Tel: 34-934017122
Fax: 34-93401770
Email: ajuanp@uoc.edu