Dr Nigel J. Miller, University of York
Edited by David Newlands
Published September 2002
1. Introduction
- 1.1 Summary of the chapter: objectives and key results
- 1.2 Top Tips: key ideas as to good practice
- 1.3 What is the purpose of questionnaires?
1.1 Summary of the chapter: objectives and key results
The aim of this chapter is to provide some practical advice on the design and implementation of questionnaires to evaluate teaching and learning in economics. The structure of the chapter is as follows:
- The next section, 1.2, offers some Top Tips: key ideas as to good practice in the administration and analysis of questionnaires and their use in evaluation.
- Section 1.3 discusses in a general way the role and purpose of questionnaires, identifying the particular strengths of questionnaires in comparison to other means of evaluation.
- Section 2 identifies the key stages in implementation of questionnaires from the initial design stage to the process of using questionnaire results to improve teaching practice. Each stage is discussed in turn. This section draws largely although not entirely from generic literature.
- Section 3 reviews the practice of questionnaire implementation in a random sample of (anonymous) economics departments in the UK, in light of the good practice guidelines discussed in section 2. As stated, the aim of the chapter is to provide practical advice that can support departments in the design and refinement of their evaluation procedures. Where there are potentially useful questions or procedures, these are identified and reproduced in detail.
- Section 4 discusses the use of electronic questionnaires, the frequency of questionnaires and issues related to confidentiality of questionnaire responses.
- Section 5 reproduces substantial parts of three questionnaires that have interesting features.
Key ideas and tips on good practice are concisely summarised, sometimes in note form, using bullet points.
Summary results – some thoughts on questionnaires and staff morale
Questionnaires and their use in academic departments are a controversial issue. Questionnaires typically contain ranked questions that are used to measure the perceived quality of specific aspects of a module and its teaching staff. Where the scores are low, this has potential to be extremely damaging to the morale (and possibly to the careers) of staff. In addition, most questionnaires contain ‘open’ questions that allow students some freedom to express their opinions about a module or tutorial programme. In a minority of cases, this is used irresponsibly and lecturers have been subjected to personal abuse. More generally, in their comments, students tend to focus on negative aspects of a module or its staff and do not necessarily evaluate the module according to the appropriate criteria, i.e. the extent to which it supports and facilitates learning.
In the way that we design and particularly in the ways that we use questionnaire results, we need to be aware of these issues. This is discussed fully in the subsequent sections, but a number of key points emerge. First, staff and students need to be clear as to the purpose of questionnaires – questionnaires comprise part of a multifaceted process whose goal is constructively to support teachers in making improvements in teaching and learning, where appropriate. They are not a mechanism for assessing the performance of members of staff, and should not be used in that way.
The practice of comparing scores across staff is totally inappropriate, and it should be made clear to staff that questionnaire results will not be used in this way. As suggested, scores are sensitive to non-appropriate criteria, and have been shown to be highly correlated to factors outside of the control of the teaching staff, such as the type of module, the background, level and year of the students, whether the module is optional or core, and exactly when in the module the questionnaire is implemented.
It is standard practice for students to submit their responses to questionnaires anonymously. It is argued that this approach increases the rate and quality of response. In this chapter, it is suggested that departments might consider relaxing the confidentiality of questionnaires, and oblige or request students to put their name to at least some of their responses. It is argued that anonymity may induce disingenuous responses that ultimately threaten the whole process and the objective of improving the teaching and learning experience. Positive effects of removing anonymity are that students are encouraged to articulate their concerns and ideas in a constructive and open manner, and there is a basis for dialogue and feedback after the questionnaire is submitted.
As stated, the purpose of questionnaires is to improve teaching and learning. To achieve this, teachers should receive some possibly informal training in how to read, interpret and respond to questionnaire responses. This is particularly relevant to inexperienced staff.
1.2 Top Tips: key ideas as to good practice
- The purpose of questionnaires is to support teachers in making improvements in teaching and learning.
- Questionnaires are not a mechanism for assessing the performance of members of staff.
- Departments should not compare scores across staff.
- Teachers should receive some kind of instruction in how to interpret and respond to questionnaire responses.
- Open and closed questions elicit different kinds of information and most questionnaires should contain both.
- Closed questions are efficient mechanisms for gleaning information about a range of specific issues.
- Open questions allow students the freedom to discuss what matters most to them and to elaborate on answers provided to closed questions.
- It may be useful to comprise questionnaires of two separate and detachable sections – for example, two A4 sheets. The first contains closed and ranked questions and is submitted anonymously; the second contains open questions and students are requested to identify themselves with these responses.
- There is nothing wrong with ranked questions that elicit responses on an ordered scale – for example, from 1 to 5 – although they have to be used appropriately.
- In analysing them the useful statistics are the proportion of respondents responding in each category.
- Constructing average scores (i.e. averaging the scores for each question across all respondents) is not a sound statistical approach.
- Computing single scores from a pool of questions is fraught with difficulties and can only work in an extremely well-designed questionnaire with a precise objective used in the right way.
- Before designing the questionnaire, think carefully about what kinds of information might be useful – too many questionnaires contain questions that are inappropriate and this is frustrating to the respondents.
- On the questionnaire, group questions into themes – this makes it more comprehensible and attractive to respondents. Questions can be grouped under the following key themes (these are discussed in more depth in section 3.1):
- overall quality indicators;
- open questions;
- student behaviour and status;
- the module;
- skills of the lecturer;
- reading and facilities;
- contribution to learning.
- Make the questionnaire attractive – this will increase the rate and quality of response.
- When analysing questionnaire responses, do not read too much into the results.
1.3 What is the purpose of questionnaires?
As a mechanism for obtaining information and opinion, questionnaires have a number of advantages and disadvantages when compared with other evaluation tools. The key strengths and weaknesses of questionnaires are summarised in bullet points below. In general, questionnaires are effective mechanisms for efficient collection of certain kinds of information. They are not, however, a comprehensive means of evaluation and should be used to support and supplement other procedures for evaluating and improving teaching.
Advantages of questionnaires
- They permit respondents time to consider their responses carefully without interference from, for example, an interviewer.
- Cost. It is possible to provide questionnaires to large numbers of people simultaneously.
- Uniformity. Each respondent receives the identical set of questions. With closed-form questions, responses are standardised, which can assist in interpreting from large numbers of respondents.
- Can address a large number of issues and questions of concern in a relatively efficient way, with the possibility of a high response rate.
- Often, questionnaires are designed so that answers to questions are scored and scores summed to obtain an overall measure of the attitudes and opinions of the respondent.
- They may be mailed to respondents (although this approach may lower the response rate).
- They permit anonymity. It is usually argued that anonymity increases the rate of response and may increase the likelihood that responses reflect genuinely held opinions.
Disadvantages of questionnaires
- It may be difficult to obtain a good response rate. Often there is no strong motivation for respondents to respond.
- They are complex instruments and, if badly designed, can be misleading.
- They are an unsuitable method of evaluation if probing is required – there is usually no real possibility for follow-up on answers.
- Quality of data is probably not as high as with alternative methods of data collection, such as personal interviewing.
- They can be misused – a mistake is to try to read too much into questionnaire results.
2. The process of designing and implementing questionnaires
In this section, the key stages of implementing a questionnaire are discussed. In section 2.1, I discuss best practice in the design of questionnaires – examples are used to illustrate where appropriate. Section 2.2 looks at the administration of questionnaires and how best to obtain a good level of response. Sections 2.3 and 2.4 review issues related to the analysis of questionnaire responses and the use of results to improve teaching. All of the material is entirely relevant to use of questionnaires in economics, but the approach is generic and illustrates with examples drawn from various uses of questionnaires. Section 3 of the chapter is devoted to analysis of questionnaire use and practice in economics.
- 2.1 Designing questionnaires
- 2.2 Administering questionnaires
- 2.3 Analysing the results of questionnaires
- 2.4 So what? Using the results of questionnaires to improve teaching and learning
2.1 Designing questionnaires
This section contains extensive guidelines on how to design a questionnaire. They are developed in simple headers and bullet points, which, I hope, will make this material more accessible and of practical benefit to potential users. There are many useful texts and guides to designing questionnaires, such as Newell (1993), Burns (2000), Bloom and Fischer (1982) and Kidder and Judd (1986).
Getting started
Before you start to design a questionnaire, identify its objectives. More specifically, identify what kind of information you want to obtain. Then brainstorm – write down all possible questions for incorporating in the questionnaire.
Constructing questions
This is the most difficult part of developing a questionnaire. Here are some useful rules of thumb to follow:
- Keep questions simple. Avoid ambiguous, leading, double-barrelled and hypothetical questions, double-barrelled questions being ones that ask two questions in one.
- Avoid words of more than three or four syllables and over-long sentences.
- In closed questions, allow the respondent the option of answering with ‘not appropriate’, ‘don’t know’ or ‘have no strong feelings’. This helps the respondent and avoids difficulties later in interpreting questions that have no responses.
- Avoid overly sensitive questions – you are unlikely to get a ‘true’ response.
Use of open and closed questions
Most questionnaires contain both types of question and this is advisable. Closed and open questions are appropriate in different contexts and provide different kinds of information.
Closed questions
Closed questions are questions in which all possible answers are identified and the respondent is asked to choose one of the answers. In the following example, students were asked to evaluate the quality of programme materials (handouts, etc.) by a series of five closed questions. (The questionnaire is not well designed but illustrates clearly the nature of closed questions.)
Example 1
Help us measure the success of the programme. Please tick one box for each of the questions.
| Programme materials | Excellent | Good | Fair | Poor | Unable to judge |
|---|---|---|---|---|---|
| 1) the availability of the materials | |||||
| 2) the quality of the materials | |||||
| 3) the durability of the materials | |||||
| 4) the quantity of the materials | |||||
| 5) the suitability of the materials for students |
Source: Fitz-Gibbon and Morris (1987), p. 62.
Advantages of closed questions
- Closed questions are an appropriate means of asking questions that have a finite set of answers of a clear-cut nature. Sometimes this is factual information but closed questions are also used for obtaining data on attitudes and opinions (see ranked closed questions below).
- They oblige the respondent to answer particular questions, providing a high level of control to the questioner.
- They involve minimal effort on the part of the respondent.
- They provide uniformity of questions and student responses, so they are potentially easier for evaluating the opinion of the sample group as a whole.
- They save time. Closed questions are less time consuming for respondents to complete, and this allows the questionnaire to ask more questions.
- They avoid problems of interpreting respondents’ handwriting.
- They can provide better information than open-ended questions, particularly where respondents are not highly motivated.
Disadvantages of closed questions
- Closed questions are appropriate only when the set of possible answers are known and clear-cut.
- If poorly designed, closed questions may be misleading and frustrate respondents. Typical problems are poorly designed questions, inappropriate questions and questions that have answers other than those listed.
Closed questions with ranked answers
- These are closed questions for which answers are located on a scale of alternatives. This type of question is often used in evaluation to uncover respondents’ attitudes and opinions. The scale often represents degrees of satisfaction with a particular service or degrees of agreement with a statement.
- Always balance scales around a mid-point in the response answer. For example, respondent may choose from the following alternatives: strongly agree, agree, have no strong feelings, disagree, strongly disagree.
Advantages of ranked questions
- The advantages of using closed questions apply – see above.
- Answers can be pooled across students to derive summary statistics that potentially measure an overall degree of satisfaction/agreement.
- Summary scores can also be obtained from pooling across different questions related to some overriding issue.
Disadvantages of ranked questions
- Attitudes and opinions are complex and not readily summarised in a scale.
- Ranked questions do not provide means for students to elaborate on or explain reasons behind the stated degree of satisfaction.
- Summary statistics are powerful and if based on poorly designed questionnaires can be damaging.
The following are examples of ranked closed questions drawn from questionnaires used to evaluate teaching in anonymous economics departments.
Example 2
Fill in one response for each question.
5 = Excellent, 4 = Very Good, 3 = Satisfactory, 2 = Fair, 1 = Poor
Skill of the instructor
| 1) Instructor’s effectiveness as a lecturer | 1 | 2 | 3 | 4 | 5 |
| 2) Clarity of instructor’s presentations | 1 | 2 | 3 | 4 | 5 |
| 3) Instructor’s ability to stimulate interest in the subject | 1 | 2 | 3 | 4 | 5 |
Example 3
For each of the following questions, please ring your answer.
The module as a whole
| 1. | The module stimulated my interest |
| Disagree 1 2 3 4 5 Agree | |
| 2. | The module was |
| Too easy 1 2 3 4 5 Too hard | |
| 3. | The module objectives were fulfilled |
| Disagree 1 2 3 4 5 Agree |
Example 4
This is an example of how ranked questions may be pooled to generate an overall index (from Henerson et al., 1987):
Teachers in a new experienced-based science programme filled out a questionnaire about each of several children in their classes. Here is a portion of the questionnaire:

The scores for questions 2, 3, 4 and 5 were summed to obtain ‘an enthusiasm index’ for each child, a point on a scale of 4–20. There are difficulties designing and interpreting these results, of course. We have to be sure that every question used in computing the index indeed reveals information about a student’s level of enthusiasm, and that the scales of the questions are consistent, i.e. that high enthusiasm is always indicated by scores close to or equal to 5. The greatest difficulty lies in interpretation of the final scores – usually researchers consider scores above or beneath threshold levels as revealing something definite about behaviour and attitudes, but it is difficult to know where to fix the thresholds. The alternative approach here would be to ask teachers to rate the enthusiasm of students.
Open questions
Open questions are questions that allow the respondent to answer in any way they wish. For example, students might be asked to respond to the following question: ‘What do you feel is the best thing(s) about the course?’
Advantages of open questions
- Flexibility. The respondent can answer in any way he/she wishes.
- They may be better means of eliciting true opinions/attitudes and identifying how strongly attitudes are held or not.
Disadvantages of open questions
- They require more thought and time on the part of respondent and analyst. This dramatically reduces the number of questions that the questionnaire can realistically ask.
- It is more difficult to pool opinion across the sample when questionnaires use open questions.
- Respondents may answer in unhelpful ways.
Open versus closed questions
‘. . . closed questions should be used where alternative replies are known, are limited in number and are clear-cut. Open-ended questions are used where the issue is complex, where relevant dimensions are not known, and where a process is being explored’ (Stacey, 1969).
Most questionnaires are ‘mixed’, containing both open and closed questions. This is often the best approach, avoiding an overly restrictive questionnaire and one that is too open and difficult to analyse. Open-ended questions can be used by students to elaborate on the reasons underlying their answers to the closed-form questions.
Supporting text
All questionnaires must be supported with some text. This should contain the following features:
- The purpose of the questionnaire should be communicated clearly to potential respondents.
- Where deemed appropriate, the confidentiality of responses should be assured.
- The supporting text should contain simple instructions on how to complete.
- At the end of the questionnaire it is a nice touch to thank the respondent for his/her time and consideration.
Questionnaires should be attractive
- Warm-up questions are recommended. These are questions that are simple to answer, such as questions on the age of student, year of study, degree programme, etc. Use of such questions makes it less likely that the respondent will disengage from the questionnaire.
- A good questionnaire has a coherent structure. Where possible, collect questions under definable subject areas and develop a logical order of questionnaires.
- Do not leave important questions to the end of questionnaire.
- Do not split questions over pages, or ask questions that require answers to be completed on subsequent pages.
- Do not overcrowd the questionnaire with questions and text.
Length of the questionnaire
- It is advised that questionnaires should not be too long (for obvious reasons). However, the appropriate length does depend upon the purpose of the questionnaire, the type of respondents targeted and the type of questions.
- Appropriately chosen and designed closed questions are easy to answer, so you can have more of them.
- For the validity of the questionnaire, it is often appropriate to include a number of questions relating to one broad issue.
Testing questionnaires
It is essential that questionnaires are thoroughly tested prior to use. Bloom and Fischer (1982) identify five key criteria that may be used in evaluating the quality of a questionnaire – these are listed and discussed below. To evaluate a questionnaire effectively, it should be tested on an appropriate sample, which, in our case, is a sample of students. Test results are analysed and any changes to the questionnaire made. After initial implementation, questionnaires should continue to be evaluated as an ongoing process.
The criteria to use in evaluating a questionnaire are:
- Purpose. In evaluating a questionnaire, one has to be absolutely clear about the purpose.
- Often, insufficient thought is given to the purpose of a questionnaire. Designers need to identify at the outset what kinds of knowledge they are trying to obtain from the questionnaire.
- Directness. Questionnaires should be as direct as possible, i.e. they should ask questions that address as directly as possible the issues you want to evaluate.
- Utility. This criterion relates to the practicalities of implementing and using a questionnaire. Questions to consider include:
- Is the questionnaire easy to administer, score and interpret?
- What resources are involved in implementing the questionnaire?
- Reliability. A study is reliable if similar results would be obtained by others using the same questions and using the same sampling criteria.
- Where questionnaires are administered at the beginning of the lecture, the sample is biased towards those students who attend lectures – of course, this bias may raise the quality of responses!
- Validity: A study is valid if it actually measures what it sets out to measure.
- Here, much depends on the quality of the questioning.
2.2 Administering questionnaires
The key elements of the process of implementing and making successful use of questionnaires in teaching can be summarised as follows:
- Agree schedule of courses and modules to receive questionnaires.
- Prepare students.
- Administer questionnaire.
- Analyse questionnaires.
- Write summary report of questionnaire and determine plan for course improvements.
- Report to stakeholders, including students.
- Implement action plan.
- Review changes made to the course in light of questionnaire.
In this section, I discuss the administration of questionnaires, i.e. the process by which students receive and submit their questionnaires. In the subsequent sections, 2.3 and 2.4, I shall discuss the analysis of questionnaires, how results are used to improve teaching and the feedback of results to students and other stakeholders. Successful implementation of all stages of the process of evaluation requires active involvement of various individuals or groups; this is summarised in Figure 1. Lecturers are primarily responsible for administering, evaluating and acting upon the questionnaire. Students are responsible for answering the questionnaire and, together with the responsible authority within the department, for ensuring that their views are heard and acted upon.
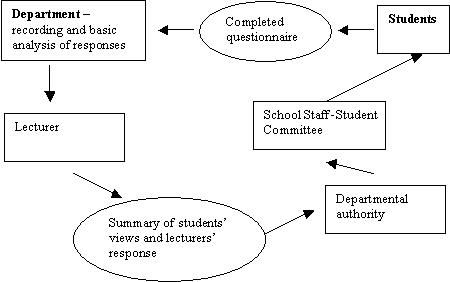
Figure 1 Questionnaires: the process of evaluation
Administering questionnaires
A criterion for successful questionnaires is maximisation of the student response rate. There are various ways of administering questionnaires that can help in achieving this:
- Hand out paper forms at the beginning of a lecture/tutorial and allow students time to complete and collect.
- This should take place towards the end of the course but not at times when student attendance may be relatively low, such as in the final lecture.
- Departments may insist on a specific time that lecturers hand out questionnaires to reduce scope for lecturers to bias the response rate downwards.
- It may be useful for the department/university to make a declaration that the lecturer is responsible for administering the questionnaire, and to suggest a target response rate. This should be around two-thirds of all students registered for the course or half of all students for larger courses.
- Take time to prepare students and impress upon them that the questionnaire and the process of evaluation are important. Key things to communicate to students before they complete the forms are the purpose of questionnaires and, where appropriate, the confidentiality of all responses. The administrator should explain verbally to the class (even if they have completed similar forms before).
- Students may be influenced to take the questionnaire more seriously if they are requested to do so by the head of department.
- Illustrate ways in which questionnaires have been used to improve previous courses.
- Where questionnaires are used to develop summary scores, it may be useful to demonstrate these scores and how they are derived, and to show examples of scores developed from previous questionnaires.
- All questionnaires should contain at least a paragraph at the top of the form stressing the value of questionnaires, confidentiality of responses and a courteous request for full student co-operation.
- Separate guidance notes to students are a useful device, perhaps in their student handbooks.
- Organise and provide the means for collection and return of questionnaires to the department.
- Students may take responsibility for return of forms.
- Envelopes should be provided by the department together with information on where to return the questionnaires.
2.3 Analysing the results of questionnaires
I shall assume that the questionnaires were completed and submitted for analysis in paper form. Online questionnaires are discussed in section 4.1. Here is a summary of the key stages in the process of analysing the data with useful tips – more extensive discussion follows:
- Prepare a simple grid to collate the data provided in the questionnaires.
- Design a simple coding system – careful design of questions and the form that answers take can simplify this process considerably.
- It is relatively straightforward to code closed questions. For example, if answers are ranked according to a numerical scale, you will probably use the same scale as code.
- To evaluate open questions, review responses and try to categorise them into a sufficiently small set of broad categories, which may then be coded. (There is an example of this below.)
- Enter data on to the grid.
- Calculate the proportion of respondents answering for each category of each question.
- Many institutions calculate averages and standard deviations for ranked questions. Statistically, this is not necessarily a very sound approach (see the discussion on ‘evaluating data’ below).
- If your data allow you to explore relationships in the data – for example, between the perceived difficulties that students experience with the course and the degree programme to which they are attached – a simple Chi-squared test may be appropriate.
- For a review of this test and an example, see Munn and Drever (1999) and Burns (2000) – the page references are indexed.
- You may wish to pool responses to a number of related questions. In this case, answers must conform to a consistent numerical code, and it is often best simply to sum the scores over questions, rather than compute an average score.
Preparing a grid
You will have a large number of paper questionnaires. To make it easier to interpret and store the responses, it is best to transfer data on to a single grid, which should comprise of no more than two or three sheets depending on the number of questions and student respondents. A typical grid looks like this:
| Questions | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Respondent 1 | ||||||||||
| Respondent 2 | ||||||||||
| Respondent 3 | ||||||||||
| Respondent 4 | ||||||||||
| Respondent 5 | ||||||||||
Coding data
If the answers to a question are represented on the questionnaire as points on a scale from 1 to 5, usually you will enter these numbers directly into the grid. If the answers take a different form, you may wish to translate them into a numerical scale. For example, if students are asked to note their gender as male/female, you may ascribe a value of 1 to every male response and 0 to female responses – this will be helpful when it comes to computing summary statistics and necessary if you are interested in exploring correlations in the data. It will make it much easier to analyse the data if there is an entry for all questions. To do this, you will need to construct code to describe ‘missing data’, ‘don’t know’ answers or answers that do not follow instructions – for example, if some respondents select more than one category.
Coding open questions is not straightforward. You must first read through all of the comments made in response to the open questions and try to group them into meaningful categories. For example, if students are asked to ‘state what they least like about the course’, there are likely to be some very broad themes. A number may not find the subject matter interesting; others will have difficulties accessing reading material. It may be useful to have an ‘other’ category for those responses that you are unable to categorise meaningfully.
Evaluating data
Often, it is sufficient and best simply to calculate the proportions of all respondents answering in each category. (An Excel spreadsheet is much quicker than using a calculator!) It is clear that having a category for all respondents who either don’t know or didn’t answer is very important, as it provides useful information on the strength of feeling over a particular question.
Questionnaire results are often used to compute mean scores for individual questions or groups of questions. For example, the questionnaire may ask students to rate their lecturer on a five-point scale, with 5 denoting excellent, 4 good, 3 average, 2 poor and 1 very poor. The mean score is then used as an index of the overall quality of a lecturer with high scores indicating good quality. This is not a particularly useful or legitimate approach as it assumes that you are working on an evenly spaced scale, so that, for example, ‘very poor’ is twice as bad as ‘poor’, and ‘excellent’ twice as good as ‘good’.
Often analysts add up scores over a number of related questions. For example, you may ask students ten questions related to a lecturer’s skills, all ranked from 1 to 5 with 5 indicating a positive response, and add up the scores to derive some index of the overall ability of the lecturer. Again, except in carefully designed questionnaires, this approach is inappropriate. It assumes that each question is relevant and of equal importance. Comparing scores across different lecturers and modules, this assumption is unlikely to hold. If you are interested in summative indices of quality, it may be best simply to ask the students to rate the lecturer themselves on a ranked scale.
2.4 So what? Using the results of questionnaires to improve teaching and learning
It is primarily the responsibility of the lecturer to review the responses and results of the questionnaires and these should be summarised in a summary report, which is presented to the department and to a representative student body. The key feature of the report is an ‘action plan’ indicating how the lecturer intends to act upon the findings of the questionnaire to improve the learning experience in future courses. Where no changes are envisaged, the reasons for these must be clearly stated. It is important that teachers receive some form of training in how to go about interpreting and using questionnaire results – as stated earlier, reading questionnaire responses can be a difficult process for inexperienced teachers and support should be available.
It is good practice to ensure that lecturers and tutors do not see questionnaires relating to themselves and to the modules for which they have responsibility until assessment of the module is completed. Analysis and report writing should then be done as soon as possible.
Mechanical data processing
It is possible that your questionnaire, if formatted appropriately, may be read and scored by machine, or that you can use a machine-scorable answer sheet. This can significantly reduce time involved in analysing questionnaires.
3. Questionnaires in evaluating teaching and learning in economics
- 3.1 A review of questionnaires and their use in economics
- 3.2 Better practice in questionnaire design and use in economics
3.1 A review of questionnaires and their use in economics
I have sampled a number of questionnaires in use in economics departments in the UK and have grouped questions into the following broad categories:
- overall quality indicators;
- open questions;
- student characteristics, behaviour and status;
- the module;
- the skills of the lecturer;
- reading and facilities;
- contribution to learning.
These are discussed in turn. I try to draw out the key features, illustrating with examples of questions in use. In the subsequent section, there is a broader discussion of questionnaires in economics, containing some ideas and tips regarding best practice.
Overall quality indicators
Less than half of the questionnaires sampled include questions or statements that invite students to rate the overall quality of modules and lecturers. Asking students to rate the overall quality of the lecturer is rare. The following are examples of these kinds of question and statements drawn from the sample of questionnaires reviewed:
- Overall quality of module (excellent, …, satisfactory, …, poor).
- Overall I found this a valuable course (strongly agree, …, no strong feelings, …, strongly disagree).
- My overall rating of the lecturer (excellent, …, acceptable, …, very poor).
- Give your overall assessment of each lecturer’s contribution to the course (very good, …, satisfactory, …, very poor).
- Overall this was an excellent module (agree, …, disagree).
- Overall how satisfied were you with this module? (on a scale of seven).
- In general, how helpful were the lectures? (not at all, …, very).
- To what extent were your expectations of the module fulfilled?
- In general, how useful were the seminars?
Open questions
All questionnaires contain at least one open question, although they vary significantly in the number of open questions and the proportion of open to closed questions – the largest number of open questions used is 13. I have detailed the most common questions asked – the percentage figures refer to the proportion of sampled questionnaires containing this question or a closely related question:
- What did you like most about the module? (47%)
- What did you like least about the module? (40%)
- What improvements would you suggest? (40%)
- General comments. (67%)
Other open questions used
Here is a selection of other open questions used in economics questionnaires. Some of these are probably better dealt with as closed questions (for example, the question on the technical level of the course). One questionnaire asks what textbook(s) students have bought. In the light of increasing numbers of students and difficulties accessing library resources, this is an interesting question:
- Explain in more detail your responses to ‘the closed questions’.
- Would you recommend this module to another student?
- What advice would you give a student about to embark on this module?
- What topics do you find most/least interesting?
- Did you find the technical level of the unit too high, too low or about right?
- Was the unit content roughly the same as you had expected?
- Which textbooks (if any) did you buy?
Student behaviour and status
A small proportion of questionnaires ask questions about the students’ characteristics and behaviour. The most common question of this sort concerns student attendance at lectures and tutorials. Typically students are asked to rank their level of attendance from excellent to poor.
In some cases, students are asked whether they agree or not with the following statement:
- I attended the lectures regularly. (27%)
Students may not wish to admit a level of delinquency, so responses may be biased upwards. It might help to be more precise in the question – one questionnaire asked students:
- What proportion of lectures did you attend? (25%, 50%, 75% 100%)
Other questions/statements that measure characteristics and status of students include:
- Other than time involved attending lectures and tutorials, how many hours per week did you work on the course?
- Circle your degree programme and year of study. (27%)
- Identifying a student’s degree course may, in small courses, appear to compromise confidentiality. It may be better to make the question optional.
- Have you studied mathematics A-level?
- What is your age?
- What grade do you expect to obtain from this module?
- Better understanding of students’ expectations may be valuable to teachers, although a module evaluation form may not be the best place to locate questions of this sort.
- Why did you choose the module? Was it compulsory, optional …?
The module
All questionnaires contain a number of closed questions about the structure, coherence and level of the module as a whole. The key areas of concern are:
- Interest/stimulation
- On a number of questionnaires, students are asked to respond to the following statement: ‘The course material stimulated my interest’ (strongly agree, …, strongly disagree).
- Level
- Example: ‘The overall level of the course was about right, given my background’ (strongly agree, …, strongly disagree).
- Design and organisation
- Example: ‘The course was well organised’ (strongly agree, …, strongly disagree).
- Clarity of course objectives
- Example: ‘The course objectives were clearly explained at the outset’ (strongly agree, …, strongly disagree).
- Workload
- Difficulty of material (much too difficult, …, much too easy).
- How did the level of difficulty of the material and quantity of material compare to other courses? (much more difficult, …, much easier).
- Quantity of work required (much too much, …, much too little).
- Consistency of content of course with course outline
One questionnaire contained a single question relating to the method of assessment. Students were asked:
- Are you happy with the means of assessment?
I think this is an important question simply because assessment is such a key and contentious area and may give rise to valuable information that can be used in the design of assessment procedures. The form of this particular question is not ideal, as it is very likely to induce a negative response. It would be more useful to ask students to suggest alternative forms of assessment, possibly in the form of an open question.
Skills of the lecturer
Questionnaires contain relatively few questions that relate directly to the qualities and skills of the lecturer. In many cases, questions relate to aspects of the module and it is open to interpretation whether this implies anything or not about the performance of the lecturer. For example, it is common for questionnaires to ask whether a module is interesting or intellectually stimulating – it is quite a different question to ask whether the lecturer seeks to make the course interesting or stimulating.
Questions relating to the skills of the lecturer cover the following broad areas:
- Presentation
- Speed of delivery
- Audibility
- Communication skills
- Interest
- Instructor’s ability to stimulate interest in the subject
- Organisation
- Students are asked: ‘Were lectures well prepared and organised?’
- Use of and quality of visual aids, overheads and handouts
- Examples: ‘Did the lecturer use visual aids?’, ‘Were the visual aids helpful?’
- Accessibility
- Instructor’s availability and helpfulness to students (excellent, …, very poor)
- Feedback
- Were your essays/assignments marked and returned promptly? (always, …, never)
- Has the lecturer been accessible to answer questions or give advice? (yes, …, no)
Reading and facilities
Most questionnaires ask about reading material. These are typical questions:
- Did you receive helpful guidance regarding reading material?
- Was the reading material readily available?
Some questionnaires include questions about facilities. For example, students are asked about the quality of the lecture rooms and access to computing facilities:
- The computing facilities I needed for this module were adequate (agree, …, disagree).
Contribution to learning
As the objective of the courses is to promote learning, it can be useful to ask students whether they believe the course has promoted learning and the development of key skills. It is very rare for questionnaires to address these issues, but there are some questions of this sort. For example, in one questionnaire, students were asked to rate:
- Contribution of the module to improving general analytic skills (excellent, …, very poor).
The third case study in section 5 provides the most comprehensive example of a questionnaire that addresses these issues.
3.2 Better practice in questionnaire design and use in economics
This section contains a review of the design and use of questionnaires in a sample of economics departments in the United Kingdom. I have identified various features of these that I believe are worth highlighting and which may be of use to other departments in designing or modifying their questionnaires.
The questionnaires reviewed have some common features. All but one of the questionnaires reviewed contain a number of ‘closed’ questions that require respondents to provide answers on a ranked scale of 1–5. Typically, students are asked to express a degree of agreement/disagreement with a series of statements. In some cases, students are asked to rate specific features of a course on a five-point scale from ‘excellent’ to ‘very poor’. All questionnaires contain some ‘open’ questions (or statements) that invite comments. The most common questions of this type are ‘What do you like least about the module?’ and ‘What do you like best about the module?’ All questionnaires provide space for ‘further comments’, giving students flexibility to say what they wish about the course or lecturer. Otherwise, there is significant heterogeneity in design of questionnaires, especially in the extent to which the attributes of individual lecturers are evaluated and in the use of closed questions.
Here are some observations and ideas that are worth flagging up:
1. Some of the questionnaires are much more attractive than others, in the formatting and layout of the page(s). As stated in section 3, it is always worth making a document as appealing as possible, as this will affect the response rate and the quality of the responses. A few forms use colour as background and in some of the text. Departments are always going to struggle to make students make the effort to complete forms in a useful way and touches like this can help.
2. A small proportion of questionnaires ask for information about the characteristics and behaviour of the respondent. For example, in one questionnaire, students are asked to state their degree programme, age (within specified bands) and year of study. A number of questionnaires contain question(s) about the students’ attendance at lectures. For example, students are asked to respond to the statement ‘I attended lectures regularly.’
Questions of this sort can significantly increase the usefulness of the questionnaire by revealing relationships between the characteristics or background of students and the types of responses and comments they make. For example, information on the degree programme of the respondent can be especially useful in interpreting responses to questionnaires on core modules that attract large numbers of students from a variety of degree programmes and departments. The heterogeneity of students is a growing problem that all departments have to face – a particular problem for economics departments in this regard concerns the issue of mathematics and its use in courses attended by students from other degree programmes who do not have a mathematical background.
The motivation and value of questioning students’ attendance at lectures and tutorials is not clear. The answer may have an impact on how seriously the lecturer and department view the student’s responses – it may subtly influence the student’s approach to answering the questions.
3. All questionnaires should contain a paragraph or two at the top of the form explaining the purpose of the questionnaire. It is important to stress that the forms are confidential and stress to the students the constructive purpose of the questionnaire process and that it helps to improve teaching and learning for students. It is also important to explain to the students how the results of the questionnaires are analysed and disseminated. For example, it is common that a summary report and action plan are presented to a student representative committee – making this clear on the form can help to convince students that their views will be considered seriously and raise the quality of response. Most forms contain a request for students to be honest and candid in their responses.
4. The length and nature of forms vary dramatically, from four questions in one case to 27 in another. However, none exceeds two pages in length, which is relatively short for questionnaires.
5. As discussed in section 2.1, one of the questionnaires relies exclusively on open questions – the form contains the following three questions:
- What were the best features of the module?
- Where could improvements be made in the module?
- Are there any other comments you wish to make?
The questions invite discussion of the positive features of teaching and learning and, unusually, contain no questions with ranked answers. There is a means for students to express their opinions freely and express criticisms but there is no real attempt to evaluate teaching formally or to draw out specific concerns.
6. Questionnaires vary in the extent to which they directly assess the individual qualities and attributes of lecturers and tutors. In one example, students are asked to comment on the ability of the lecturer to communicate, his/her knowledge of the subject, whether the lecturer can be contacted easily and his/her level of preparedness for lectures. This is not usual, however. In most questionnaires, questions relate more to the characteristics of the module. For example, it is common to ask students to respond to the following statements:
- The lectures were clear and understandable.
- The lectures increased my understanding of the subject.
- The lectures were interesting.
It is not straightforward to know how to interpret responses to these kinds of question, and unfavourable responses do not necessarily imply anything about the qualities or efforts of the teacher. For example, if students respond that lectures are not interesting and do not increase their understanding, this may be due to the nature of the topic and the match of the module with their background and interests, or it may be due to the lecturer’s presentation and use of the material. It follows that it is probably best to include at least one question about the lecturer’s qualities.
7. One tutorial evaluation questionnaire was divided into two parts and the first part asks questions about the ‘tutorials’. Students were asked whether they considered the tutorials to be valuable and stimulating, whether the tutorials were relevant and whether students learnt from tutorials. The second part asked questions about the quality of the tutor. Students were asked about the tutor’s command of the subject, ability to communicate, accessibility and so on. Often, weaknesses in tutorials can be attributed to fundamental problems in the structure, content and methodology of the tutorial – issues that often are out of the control of the tutor. This approach can usefully distinguish between such problems and problems related to the tutor him or herself.
8. A number of questionnaires ask respondents to identify ways in which the module may be improved. This is a useful question as it most directly relates to the purpose of the questionnaire.
4. Other issues
4.1 Electronic questionnaires and computer-aided evaluation
Questionnaires may be posted online and submitted electronically. This can significantly reduce the time involved in administering and analysing questionnaires. Answers submitted on a spreadsheet can be entered on to a summary sheet and summary scores computed much more quickly when the spreadsheet is submitted electronically.
The major problem with postal or electronic mailing of questionnaires is that response rates tend to be low. Some things you can do to lessen the extent of this problem are as follows:
- Students should be introduced to computerised questionnaires in supervised computer sessions typically in their first year.
- Students should be reassured that their responses are anonymous.
- When questionnaires are posted electronically, students’ e-mail addresses and identities should be encrypted by the software program.
- Follow-up contacts are very effective: studies have shown that one follow-up contact generates 20 per cent more responses. Second and third follow-ups increase the response total by a further 10–12 per cent (Calvert, 1963; Sewell and Shah, 1968).
- It may be difficult to convince students of the confidentiality of their responses where individual responses are monitored.
- Telephone calls are particularly effective for follow-up, although this is time consuming and may not be feasible with a student population.
- The form of the follow-up call/mail can affect response rates. Do not make the respondent feel threatened, but make it clear that his/her non-response is noted.
- Some possible follow-up mails are ‘Would you believe you’re the only one who hasn’t returned the questionnaire?’, ‘Support the programme. Return your questionnaire now!’ and ‘We’re waiting to hear from you!’ (Henerson et al., 1987, p. 82).
- Timing of mailing. Do not send questionnaires at a time when students feel under pressure, e.g. around examination time.
- It has been shown that responses are more likely if the mailing is towards the end of the week.
4.2 Frequency
It may not be necessary to evaluate a module every time it is delivered. Departments may consider a biennial system – this reduces the burden of analysis and may encourage a better-quality response on the part of the students.
4.3 Confidentiality
Almost all questionnaire responses are confidential. It is widely accepted that this raises the rate of response and may encourage honesty in responses.
There are disadvantages to confidentiality, however, and it might be worth considering questionnaires that invite students to put their name to the form – I know of one questionnaire used in evaluation of economics that does this, whilst making clear that this is optional and views will be taken into account whether the form is named or not. As most lecturers have experienced, anonymity can encourage disingenuous responses and prevents the department from responding to and possibly resolving criticism, whether warranted or not. It is apparent that anonymity allows some students to make irresponsible comments and, more generally, to offload frustrations with their own learning and experience of studying economics – comments that they might not make if they had to respond personally to the department or lecturer.
5. Case studies - some examples of questionnaires in higher education
In this section, I have reproduced all or significant parts of three questionnaires. They are all currently in use in academic departments in the UK. Questionnaire 1 is a complete questionnaire and is comprised entirely of three open questions. This is an interesting approach but very atypical and it clearly does restrict the type of information that will be gleaned from the responses. I note that students are asked not to detail the worst features of the module but to suggest possible improvements – this is an attractive feature, as it tends to encourage a constructive approach to questionnaire responses.
Questionnaires 2 and 3 contained open questions but I have omitted these, choosing to focus on the structure and design of closed questions. Questionnaire 2 is unusual in the degree to which it explores the skills and abilities of the lecturer. Clearly, this is relevant information and can potentially direct teachers to areas of their teaching that they might work on. One reason I like questions of this sort is that students will want to talk about the individual characteristics of lecturers anyway, usually in responses to open questions. This approach imposes some structure to their responses. Note that the questionnaire, like most, asks some questions that will be inappropriate in many lecture situations. For example, lectures are not necessarily a good environment for ‘encouraging student participation’.
The strength of questionnaire 3 is its structure. As discussed above, clear grouping of questions under themes is helpful in the design of the questionnaire and helpful to the respondent. In addition, the questionnaire probes areas that most questionnaires do not. In particular, it asks for a certain amount of information on the students’ status and background, which is useful when it comes to interpreting the responses. Another important characteristic of the questionnaire are the questions on the perceived contribution of the module to students’ skills. This is an unusual approach but highly commendable, as it gets to the heart of what teaching is all about – facilitating skill acquisition in students.
Questionnaire 1: Lecture questionnaire
All members of the teaching and support staff in the School of Economics are committed to the provision of teaching of the highest quality and strive to ensure that this is a comprehensive, meaningful and systematic policy.
In an attempt to implement and deliver a teaching programme of the highest quality and to maintain consistency in this policy, measures exist to record how well this aim is being met. One of these measures is the direct questioning of students about the modules they have taken. This serves to give immediate, qualitative feedback to the tutor concerning his/her module content, teaching performance and administration. These results are used to alter, where the tutor deems appropriate, the module before it is delivered in the following year. Thus, this system gives students a direct input into teaching design, delivery and administration.
Please take time in writing your responses; your input is an essential part of the School’s monitoring process and thus an integral part of the policy of maintaining and extending teaching quality.
Module Title………………………………………………………………………….
Lecturer …………………………………. Semester ………………………………..
What were the best features of the module?
Where could improvements be made in the module?
Are they any other comments you wish to make?
Questionnaire 2: Lecture questionnaire
The purpose of this questionnaire is to obtain your views and opinions about the lectures you have been given during the course to help the lecturer evaluate his/her teaching.
Please ring the response that you think is most appropriate to each statement. If you wish to make any comments in addition to these ratings please do so on the back page.
| The Lecturer: | Strongly Agree | Agree | No Strong Feelings | Disagree | Strongly Disagree |
|---|---|---|---|---|---|
| 1. Encourages students to participate in classes. | 5 | 4 | 3 | 2 | 1 |
| 2. Allows opportunities for asking questions. | 5 | 4 | 3 | 2 | 1 |
| 3. Has an effective lecture delivery. | 5 | 4 | 3 | 2 | 1 |
| 4. Has good rapport with learners. | 5 | 4 | 3 | 2 | 1 |
| 5. Is approachable and friendly. | 5 | 4 | 3 | 2 | 1 |
| 6. Is respectful towards students. | 5 | 4 | 3 | 2 | 1 |
| 7. Is able to teach at the students’ level. | 5 | 4 | 3 | 2 | 1 |
| 8. Enables easy note-taking. | 5 | 4 | 3 | 2 | 1 |
| 9. Provides useful handouts of notes. | 5 | 4 | 3 | 2 | 1 |
| 10. Would help students by providing printed notes. | 5 | 4 | 3 | 2 | 1 |
| 11. Has a wide subject knowledge. | 5 | 4 | 3 | 2 | 1 |
| 12. Maintains student interest during lectures. | 5 | 4 | 3 | 2 | 1 |
| 13. Gives varied and lively lectures. | 5 | 4 | 3 | 2 | 1 |
| 14. Is clear and comprehensible in lectures. | 5 | 4 | 3 | 2 | 1 |
| 15. Gives lectures which are too fast to take in. | 5 | 4 | 3 | 2 | 1 |
| 16. Gives audible lectures. | 5 | 4 | 3 | 2 | 1 |
| 17. Gives structured and organised lectures. | 5 | 4 | 3 | 2 | 1 |
| 18. Is enthusiastic about the subject. | 5 | 4 | 3 | 2 | 1 |
Questionnaire 3: Student module evaluation
Your responses to this form are completely anonymous. Data will not be available to instructors until after module grades are recorded.
Instructor’s full name: …………………………………………..
Module’s full name: …………………………………………….
Semester (term, year): ………………………………………….
Fill in one response for each question below.
Excellent (High) = 5, Very Good = 4, Satisfactory = 3, Fair = 2, Poor (Low) = 1
LEVEL OF EFFORT | |||||
| 1. Level of effort you put into the module. | 1 | 2 | 3 | 4 | 5 |
SKILL OF THE INSTRUCTOR | |||||
| 2. Instructor’s effectiveness as a lecturer and/or discussion leader | 1 | 2 | 3 | 4 | 5 |
| 3. Clarity of instructor’s presentations | 1 | 2 | 3 | 4 | 5 |
| 4. Organisation of instructor’s presentations | 1 | 2 | 3 | 4 | 5 |
| 5. Instructor’s ability to stimulate interest in the subject | 1 | 2 | 3 | 4 | 5 |
| 6. Instructor’s ability to deal with controversial issues judiciously (such as: ethnicity, race, gender) | 1 | 2 | 3 | 4 | 5 |
RESPONSIVENESS OF THE INSTRUCTOR | |||||
| 7. Instructor’s availability and helpfulness to students | 1 | 2 | 3 | 4 | 5 |
| 8. Instructor’s respect for student ideas | 1 | 2 | 3 | 4 | 5 |
| 9. Usefulness of instructor’s oral and/or written feedback | 1 | 2 | 3 | 4 | 5 |
WORKLOAD AND STRUCTURE OF THE MODULE | |||||
| 10. Difficulty of material (1 = much too easy, 5 = much too difficult) | 1 | 2 | 3 | 4 | 5 |
| 11. Quantity of work required (1 = much too little, 5 = much too much) | 1 | 2 | 3 | 4 | 5 |
| 12. Clarity of module’s objectives | 1 | 2 | 3 | 4 | 5 |
CONTRIBUTION TO LEARNING | |||||
| 13. Value of assigned materials | 1 | 2 | 3 | 4 | 5 |
| 14. Value of book lists and references | 1 | 2 | 3 | 4 | 5 |
| 15. Contribution of this module to improving your general analytic skills | 1 | 2 | 3 | 4 | 5 |
| 16. Contribution of this module to broadening your perspective | 1 | 2 | 3 | 4 | 5 |
| 17. Contribution of this module toward your knowledge of individual areas of study | 1 | 2 | 3 | 4 | 5 |
| 18. Contribution of this module to the degree programme | 1 | 2 | 3 | 4 | 5 |
OVERALL QUALITY OF THE MODULE | |||||
| 19. Overall quality of module | 1 | 2 | 3 | 4 | 5 |
STUDENT STATUS | |||||
| 20. Year (1 = First Year, 2 = Second Year, 3 = Third Year, 4 = Postgrad., 5 = Part-time | 1 | 2 | 3 | 4 | 5 |
| 21. Programme (1 = Economics, 2 = Joint, 3 = Another Dept., 4 = Exch., 5 = Postgrad. or Part-time) | 1 | 2 | 3 | 4 | 5 |
MISCELLANEOUS | |||||
| 22. What grade do you expect to receive in this module? (1 = Fail, 2 = 3rd, 3 = 2:2, 4 = 2:1, 5 = 1st.) | 1 | 2 | 3 | 4 | 5 |
| 23. Why did you choose this module? (1 = Interest (elective), 2 = Elective, 3 = Dept. requirement, 4 = University requirement, 5 = Other | 1 | 2 | 3 | 4 | 5 |
| 24. Would you recommend this module to others? (1 = Yes, 2 = No) | 1 | 2 | |||
References
Bloom, M. and Fischer, J. (1982) Evaluating Practice: Guidelines for the Accountable Professional, Prentice Hall, New Jersey.
Burns, R. (2000) Introduction to Research Methods, 4th edn, Sage, London, pp. 566–94.
Calvert, R. (1963) Career Patterns of Liberal Arts Graduates, Carroll Press, Cranston, RI.
Fitz-Gibbon, C. and Morris, L. (1987) How to Design a Program Evaluation, Sage, London.
Henerson, M., Morris, L. and Fitz-Gibbon, C. (1987) How to Measure Attitudes, Sage, London.
Kidder, L. and Judd, C. (1986) Research Methods in Social Relations, CBS College Publishing/Holt, Rinehart and Winston.
Munn, P. and Drever, E. (1999) Using Questionnaires in Small-scale Research, SCRE Publication 104.
Newell, R. (1993) ‘Questionnaires’, in N. Gilbert (ed.), Researching Social Life, Sage, London, pp. 94–116.
Sewell, W. and Shaw, M. (1968) ‘Parents’ education and children’s educational aspirations and achievements’, American Sociological Review, vol. 33(2), pp. 193–209. JSTOR 2092387
Stacey, M. (1969), Methods in social research, Pergamon Press, Oxford.
