Volume 11, Issue 1, 1997
Linear Programming on the Web
- Ziggy MacDonald
- University of Leicester
Introduction
In previous issues of this journal I have written about the Excel Solver add-on as an appropriate and powerful medium for teaching linear programming (MacDonald 1995 & 1996). Estelles et al (1996) have also written about the virtues of GAMS as a tool for teaching mathematical programming. However, the time is probably right to look beyond the traditional teaching mediums and consider what is available on the internet, particularly the World Wide Web. There appears to be quite a wealth of linear programming (LP) related material on the web, however, much of it is directed at practising researchers. Fortunately there is some growth in the available teaching material and subsequently this article will consider what is currently available with a view to what we might expect in the very near future.
OR/MS Sites
There tends not to be specific linear programming sites on the web, rather, LP material is typically found under more general collections of operations research/management science (OR/MS) resources. There are, as you would expect, a considerable number of OR related sites. Michael Trick's Operations Research Page provides a very comprehensive guide to these but it does require some skilful searching to seek out the LP-related material. However, for the purposes of writing this paper, it is rather fortunate that there appears to be three very large sites that dominate the web. These can be found at the World-Wide-Web for Operations Research and Management Science (WORMS) , the Optimisation Technology Center (OTC) and the Institute for Operations Research and the Management Sciences (INFORMS). Given the quality of material on the first two of these sites these will form the focus of this paper although reference will be made to the latter. All of these sites provide a rich resource for an introductory exploration of LP (and most other OR topics) although much of the material goes well beyond the needs of most undergraduate courses. The WORMS site is based at the University of Melbourne and is run by the graduate students of the Operations Research Group (under supervision by Moshe Sniedovich). The site contains a lot of material for student exploration including a virtual encyclopaedia which is continually being added to by OR/MS practitioners around the word. Of particular relevance is the section concerning interactive solvers which will be considered in more detail later. The Optimisation Technology Center, founded in 1994, is a joint enterprise of the Argonne National Laboratory and Northwestern University. This site has a wealth of material including information about optimisation algorithms and applications, software packages, and a collection of case studies, some of which are fully interactive (an interactive Diet Problem case study is considered later). The INFORMS site is the internet manifestation of the merged OR Society of America and The Institute of Management Science. It has a large section dedicated to education and offers traditional support material (e.g. instructional videos) in addition to published material and bibliographic services. It doesn't, however, offer the truly interactive features that the other two sites have to offer which are the subject of the following section.
On-Line Simplex
For the teaching of Simplex, the OTC has its impressive Simplex Java Applet. With this tool, a student can enter a problem with a maximum of seven variables and seven constraints, and step through the simplex method to find its solution. This type of interactive web material is undoubtedly the way forward for web-based teaching resources, the typical alternative that is currently available being the standard page where a student can download documents which will ultimately be printed off and used away from the computer. Before I describe the tool I should offer a word of warning. In the first place, the Applet is very sensitive and I did have difficulty in getting it to do anything initially (http://www-c.mcs.anl.gov/home/otc/Guide/CaseStudies/simplex/index.html an older version is also available which appears to be slightly more stable) [I cannot find the older version - web editor]. What is more, because it makes use of Applet windows, it is very easy to be fooled into thinking that nothing is happening when you click the button to enter a new problem. You do not get an hour glass suggesting that something is happening, rather, if you sit and be patient a small window will appear in time prompting you to define the problem dimensions. What is more difficult is getting rid of the windows once you have completed the problem, but I believe these minor irritations will disappear as the technology evolves. Returning to the tool, to start the routine the user clicks the 'New Problem' button from the web page and a small window appears in which the user describes the LP model in terms of the number of variables and constraints with the use of some input boxes. Following this the user is presented with the window shown in Figure One in which the LP equations can entered via a combination of input boxes and drop-down list-boxes. This is one of the attractive features of Java scripting although one should be aware of the lack of error-trapping facilities (you can, if you so desire, enter any old rubbish in the boxes, which is true of any Java application).
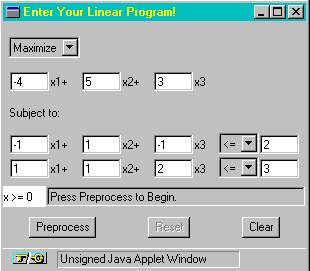
Figure One: Linear Program Input Box
Having entered the problem formulation the user clicks the 'Preprocess' button which reveals the problem in simplex form via another Applet Window, shown in Figure Two, which reveals the initial basic feasible solution.
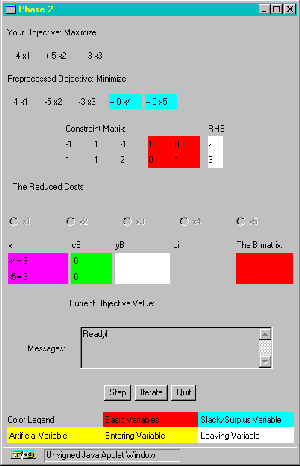
Figure Two: Simplex Formulation of the Problem
At this point the user can then choose how to proceed to the optimal solution. The 'Step' method allows the user to get involved with the solution generating process by determining the entering variable. At this point, I have to confess that I became just a little confused as the display did not appear to update between steps, although the message window did give some indication of what was going on. What is important, however, is that this is a clear indication of what is possible on the web and it suggests to me that as Java scripting develops, the sophistication of this type of material will greatly improve.
The other main site (WORMS) has put considerable effort in exploring the capabilities of Java scripting with its experimental JAVA section. This appears to be their 'work-in-progress' space (note) and an attempt has been made to reveal the efforts required to get Java to do the things that we want from the web. The real stuff of interest, however, is not available directly from WORMS (as far as I can tell), as it appear that the more advanced developments of this technology are available from "Simplex Place", a site written by the same author (Moshe Sniedovich) which lives on the same server. The end result is perhaps unrivalled on the web. In addition to a detailed explanation of the theory of the simplex method (written in a readable and lively style), the site provides an interactive simplex tool created with JavaScript which is embedded in the web page, removing the possible confusion of Applet windows floating around. It's a similar animal to the OTC's impressive Simplex Java Applet, but it lives in a far richer teaching environment and has more in common with the traditional methodological approach of textbooks. This is the essence of my particular attraction to this site. The user can discover the simplex method from the first principles of gaussian elimination, through the determination of entering variable (referred to as the Greedy Rule!) and leaving variable to the optimality test, and at each stage of the learning process there is a Java tool for practising the methods (with OTC's Simplex Applet, the instructional material is separate from the interactive tool). Having worked through this support material the user can then proceed to interact directly with each tableau on the road to a final solution. This is illustrated in figure Three.
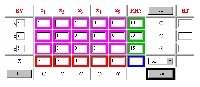
Figure Three: Interactive Tableau
The student makes use of the tool in Figure Three as though it were a traditional simplex tableau (unlike that provided by OTC). In terms of learning, the student can use this tool to check all the calculations for each set of row operations required to pivot each tableau. What is particularly promising about this site is the author's obvious desire to keep on improving the tool. Promised features include a facility to describe the order of the problem and the ability to deal with 'greater than or equal to' constraints explicitly (i.e. by utilising the Big M tableau method). If this occurs by the time I teach the subject next academic session I will certainly be recommending this site to my students (in addition to Excel Solver!).
On-Line Graphical Method
The site that gave me the most excitement (I was even driven to email the author to communicate this excitement!) was concerned with the graphical method for solving LPs. The site in question is called "Anima-LP: A Tool for teaching Linear Programming". (http://weber.u.washington.edu/~cvj/animalp.html)[Now at http://www.cs.stedwards.edu/~wright/linprog/AnimaLP.html - web editor]. Based at The School of Business Administration, University of Washington, and written by Chris Jones, this is a fantastic innovation in web-based interactive teaching. This Java application (also available to download as a fully featured MAC package) is designed to allow students to manipulate an LP and observe the effect on the graphical solution in real-time. The basic tool, which consists of an input tool and a graphical solution space, is shown in Figure Four.
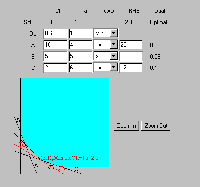
Figure Four: On-Line Graphical Solution
In Figure Four one can see the graphical solution to the 'Diet Problem', previously discussed in MacDonald (1996) and Estelles et al (1996), as created with this interactive tool. Not only can students enter the constraints etc. via a spread-sheet like interface and observe the corresponding graphical representation as it changes, the application is written such that one can directly alter the constraints by clicking and dragging the graphical view. As the graphical view is manipulated, the problem definition given above it is automatically resolved. Although the on-line version is perhaps a little sensitive (you have to remember to press enter after each change you make in the problem definition) this is clearly the way forward for interactive web-based teaching. Not only would I recommend this site to anyone charged with introducing students to linear programming, I will certainly be referring my third year business economics to this page.
On-Line Solvers
Another particularly exciting development on the web is the development of powerful on-line solvers, not intended for instruction and certainly capable of handling large problems. The OTC has an excellent example of this via its system referred to as the Network-Enabled Optimisation System - NEOS. Not limited to linear programming, the NEOS server has solvers for unconstrained optimisation, stochastic linear programming, bound constrained optimisation, non-linearly constrained optimisation and linear net work optimisation. Although one is required to input problems in MPS format (note), using the on-line solvers is very straightforward, and given that the output is returned very quickly (both over the web and via a separate email) they can be demonstrated live in a lecture theatre. Having said this, this unique resource at NEOS is most likely to be more suitable for project-based work for more advanced students.
Miscellaneous Material
The case studies at OTC are a promising development although at present there is only one available for LP (The Diet Problem!). The user can work through the formulation of a diet problem and can then proceed to interact with the problem by choosing from a list of foods (with accompanying details on price and nutritional information) those which are to be included in the problem. In my first attempt I selected raw broccoli and lettuce. The tool informed me that this was infeasible as I could not meet my minimal nutritional requirements (no wonder I permanently feel ill!). The point is that users can select a basket of foods, alter the nutritional constraints if so desired, and find the optimal choice with associated minimum cost. The user can then proceed to analyse the problem solution further and look at the sensitivity information and a breakdown of the nutritional contribution of each food in the final solution. Overall this is a useful resource but it does requires some careful experimentation to be useful as an instructional tool.Other miscellaneous resources include the Imperial College Management School OR-Library, maintained by John Beasley. This library contains data-sets for a variety of OR type problems from assignment problems to vehicle routing problems. The LP section contains twenty seven data files, but beyond this the material is of limited value. Perhaps of greater use is the Mathematical Programming Glossary, maintained by Harvey Greenberg. The site contains material contributed by a variety of sources (including a lot of LP-related material) and is excellent for brief but detailed information on all aspects of mathematical programming. Finally there is the standard LP FAQ (Frequently Asked Questions). The OTC maintains these for LP and they provide a useful resource for students wishing to gain an introductory insight into the world of LP.
Concluding Remarks
The quantity and quality of LP material available on the web, like other subjects, appears to expand on a daily basis. The sites mentioned in this paper can only represent a snapshot of what is currently available and is certainly not exclusive. The selective list presented here was a deliberate choice, simply intended to highlight the quality of material that can be found. The new direction for the web is interaction beyond simple clicking of links. The Java revolution is much hailed and, although far from being fully exploited, the use of it exhibited by the sites mentioned here is promising. I expect to see more developments in this direction with students having access to interactive web facilities that go well beyond the constricts of traditional instruction.
References
Estelles, T. C., Arre, M. M. & Garrido, R. S., 1996, "Economic Optimisation with GAMS", Computers in Higher Education Economic Review, 10 (2) 2-7MacDonald, Z., 1995, "Teaching Linear Programming using Microsoft Excel Solver", Computers in Higher Education Economic Review, 9 (3) 7-10
MacDonald, Z., 1996, "Economic Optimisation: An Excel Alternative to Estelles et al's GAMS Approach.", Computers in Higher Education Economic Review, 10 (3) 2-5
Notes
As an aside, I did get a bit lost on this page as I often do at sites that make extensive use of frames. I fail to see why web page designers believe that half a dozen frames with one web page will somehow enhance the accessibility of the material. Hopefully, as the web develops, authors will start to adhere to the rules that apply to software interface design whereby navigation is at the top of the list of considerations during development.
MPS format is the de facto standard ASCII medium among most of the commercial LP codes. MPS input format was originally introduced by IBM to express linear and integer programs in a standard way. The main feature of MPS format is that
it is a fixed column format (as opposed to entering the model as equations), and everything (variables, rows, etc.) gets a name, thus care must be taken that all information is placed in the correct columns.
Department of Economics
University of Leicester
University Road
Leicester. UK
LE1 7RH
E-mail abm1@le.ac.uk

