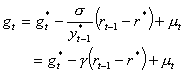Appendix
Appendix to "Modifying the Taylor–Romer Model of Macroeconomic Stabilisation for Teaching Purposes" by Ross Guest
This appendix provides the derivation of the growth form of the IS curve (equation (1)) and the Phillips curve (equation (3)).
The Phillips curve is typically expressed in terms of inflation and unemployment as follows (symbols are as defined in the text unless indicated):
where u is the unemployment rate and u* is the NAIRU.9 It is assumed that πt – 1 = π* , where π* is the expected rate of inflation and expectations are backward looking. We then invoke Okun’s Law, which relates the change in the output growth gap to the unemployment gap as follows:
where g is the growth rate of output and g* is the output growth counterpart of the NAIRU.10 Substituting equation (A2) into equation (A1) we have the Phillips curve in the text, except that the growth rate of output has replaced the level of output:
To derive the growth form of the IS curve, we start with the conventional IS curve relationship (equation (1)):
where y and y* are the level of output and potential output, respectively, and r is the real interest rate. Define the growth rates for output and potential output as follows:
and
where g and g* are the growth rate and potential growth rate, respectively. Substituting equations (A5) and (A4) into equation (A3), and assuming yt – 1 = yt – 1* for t = 1,11 gives: