The effectiveness of remedial education – addressing enhancement in student performance and retention in a post-1992 university
Giorgio Di Pietro
Westminster Business School
Published November 2011
In recent decades many countries have experienced a significant expansion of higher education. This impressive growth has been accompanied by an increasing number of students who are perceived to be unprepared for university and college level work. In light of this situation, a large proportion of higher education institutions have been forced to set up remedial courses in literacy and numeracy for first-year students. Nevertheless, whilst in the US there is a growing debate about the effectiveness of these courses, this issue is much less questioned in the UK. In an attempt to address this deficiency, in this project I look at the effect of remediation in a large School of a post-1992 UK university. A regression discontinuity (RD) design is used in order to address the issue of non-random selection into remedial education.
My sample comprises three consecutive cohorts of first-year students in the academic years 2007-2008, 2008-2009 and 2009-2010. All students enrolling for the first time are required to take an on-line multiple-choice diagnostic test in math. While students whose score on this screening math test is below a given cut-off value are automatically enrolled on a remedial math course, those who scored equal or above this cut-off are exempted from it. There are no exceptions to this rule. The idea of the RD design is to compare the average outcome of students whose result is just above the minimum score requirement with the average outcome of their peers who have scored just below the cut-off. Given that these two groups of students are basically thought to have the same observed (and unobserved) academic ability, the former group represents a good proxy of what would have happened to students if they had not attended remedial courses.
Because in the academic year 2009-2010 the cut-off score on the math screening test is one-point lower than that in the academic years 2007-2008 and 2008-2009, this was redefined by subtracting the cohort-specific cut-off score from each student’s score.
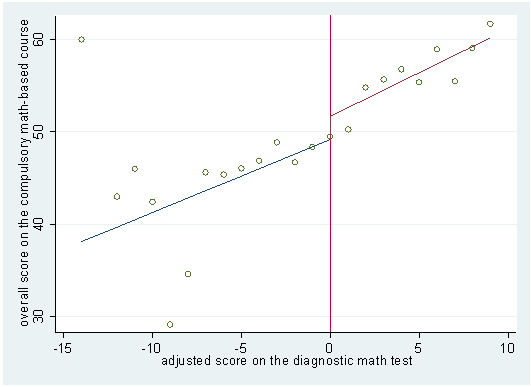
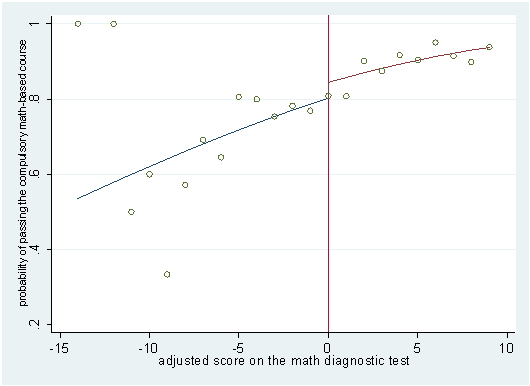
The effectiveness of the math remedial course is measured by comparing the performance of remedial and non-remedial students in a math-based course, which all first-year students are required to take. I consider two different indicators of student performance on the compulsory first-year math-based course: 1) a binary variable that takes the value 1 if the student has successfully completed the course, and zero otherwise; 2) the overall score (out of 100) received by the student on the course.
In the Figure below I depict the relationship between the adjusted score on the math diagnostic test and student performance in the compulsory first-year math-based course, using pooled data from the three cohorts. This Figure shows the raw average student outcome at each value of the adjusted score, as well as predictions from a linear model where student performance is regressed against the adjusted score on the math diagnostic test. Whilst in the upper part of the Figure student performance is proxied by the overall score on the math-based course, in the lower part of Figure a simple binary outcome (pass or fail) is used. Looking at both panels, in line with my expectations, student performance is an increasing function of the score on the math diagnostic test. However, one may note that in both panels there seems to be no discontinuity in student performance at the cut-off based on the math diagnostic test. This suggests that attending the math remedial course has no discernible impact on student performance in the compulsory first-year math-based course.
Student performance on the compulsory first-year math-based course and the adjusted score on the math diagnostic test
Additionally, my empirical results show that the effectiveness of remediation does not depend on its timing. Taking the math remedial course at the same time or prior to the compulsory math-based course does not change the conclusion mentioned above.
My findings are consistent with those of a recent study by Lagerlöf and Seltzer (2009), which is based on data from a pre-1992 UK university. Taken together, these results may call for a review of the remediation policy offered at university level in the UK.

