Dieter Balkenborg and Todd Kaplan, University of Exeter
Published September 2009
Introduction
In our experience, economic classroom experiments are a great way to introduce students to economic key concepts. They are fun for the students and for the teacher. While perfect teachers may not have to rely on anything but their charisma, both the interest of our students in the material we taught and our student evaluations improved with the introduction of this technique. In this chapter we want to discuss some effective teaching experiments and explain how and why we used them in our teaching. We will also describe how to run classroom experiments and which resources are available.
We will concentrate primarily on teaching experiments that are derived from research experiments and are hence based on a specific economic model and address a specific behavioural hypothesis. Independently there exists a tradition of using gaming, simulations and role-play in teaching. We will only occasionally refer to this approach, which is discussed (with several excellent examples) in a different chapter of the handbook.
Arguably, economics is developing into an experimental science and our teaching should appropriately reflect this development. All leading economics journals now regularly feature articles on experimental economics. The development was recognised when Daniel Kahneman and Vernon Smith obtained their Nobel prizes in 2002. Interestingly, Vernon Smith obtained his prize for showing that markets and economic theory work even under harsh conditions, while Kahneman’s work showed that the rationality assumptions underlying most of traditional economic theory do not accurately describe human behaviour even in simple decision situations.
Likewise, economic teaching experiments can be used to illustrate how economic concepts are helpful in explaining observable behaviour. They can also be used to discuss its limitations critically.
Economic experiments can be a great motivator. Vernon Smith himself was motivated in his research by his experience as a PhD student participating in market experiments carried out by Chamberlain. One of the authors became an economist because of his participation in economic research experiments. Many of the researchers who fostered the breakthrough in experimental research have started to use experiments in their teaching. In the words of Charles Holt (1999) classroom experiments have become ‘the most exciting new development in teaching economics’.
Taking advantage of this breakthrough and running your own classroom experiment is just a few keystrokes away via the Internet. It should not take more than a day to get acquainted, for instance, with Charlie Holt’s Veconlab.
There are also strong arguments that teaching experiments work most effectively in the classroom with pen-and-paper. We will compare the advantages and disadvantages of different ways of running experiments.
2. Why use economic classroom experiments?
‘The various experiments conducted made the module much more interesting, understandable and most importantly enjoyable’ (from a student evaluation).
Again, experiments are a fun way not only to learn, but also to teach. They can inspire students to learn more about a topic and provide an easy way to engage students in discussions. Stated in the terminology of Kolb (1985), they provide the concrete experience on which reflective observation can be based. The teacher can use this experience in classroom discussions and guide the students towards ‘abstract conceptualization’, i.e. the understanding of new theoretical concepts, which can then be used to analyse the data and other economic phenomena. For instance, students who have experienced cut-throat competition, in an experiment based on the Bertrand model discussed below, understand very well how zero profits arise and are a result of equilibrium. This active learning experience will last well beyond the course, in quite a different way from just seeing the theoretical analysis of the model and the claim that it is applicable in many economic situations. Seeing theory work in action helps the credibility of our science. This is further enhanced since experiments are a great way to get students closer to current research.
Another advantage of experiments is that they work well for all levels of students (even sixth form). Experiments can introduce a topic in a comprehensible way to students from many different backgrounds and skills, in particular to those with low mathematical skills.
Scientifically proven benefits
There have been a number of recent studies trying to determine the benefits of using classroom experiments. The basic methodology is to keep the lecturer and module fixed, while randomly assigning students to two groups, one with experiments and one (a control) without experiments. Afterwards, one compares performance.
Emerson and Taylor (2004) found that experiments boosted microeconomics students’ scores on a standardised test for understanding college economics, TUCE.[note 1] They found that experiments increased the scores of both females and males but helped females close the gender gap. They also found that experiments benefited the weaker students (lower grades overall). Dickie (2006) also found an overall improvement in TUCE scores by using classroom experiments.
Ball, Eckel and Rojas (2006) ran wireless experiments in a principles of economics class and found that experiments improved the overall mark on the final examination. Again, they found that the benefit was stronger for females than males. They found that the benefit was highest for first-year students. They also found that experiments significantly improved teaching evaluations of the lecturer and the degree to which students found the course stimulating.
Durham, McKinnon and Schulman (2007) and Emerson and Taylor (2004) both find that experiments benefit different personality types differently, with read-write learners benefiting less than those that prefer learning by doing.
Note
[1] The Test of Understanding in College Economics, TUCE, is a standardised, multiple choice test used in the United States at the undergraduate level, primarily targeting principles-level coursework. See https://en.wikipedia.org/wiki/TUCE.)
3. What are economic classroom experiments?
The easiest way to answer this question is with a simple example. This experiment only takes a few minutes to run.
Case 1: The guessing game (hand run)
Guess a number between 0 and 100. You will be guessing this number with 72 other people. The guess closest to two-thirds of the average number wins. Ties will be broken randomly. Please write your guess down before scrolling down.
____
Here are the results run on second year microeconomics students at the University of Exeter.
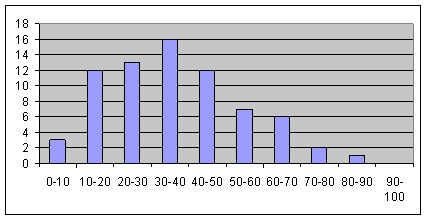
The average was 36.68. Two-thirds the average was slightly under 24.5. The winning guess was 24. Were you a winner?
After showing them the results (of the previous year), these are the questions we discussed with students: Why did you write down your guess? If you thought everyone else was choosing their numbers randomly, what would you guess? If everyone thought the same as you, what would you guess? If everyone was rational, what should they guess (i.e. the equilibrium)? There were 6 guesses above 66.667. Does it ever make sense to guess above 67?
We then asked them to guess another number under the same rules. Before scrolling down, what do you think happened to the guesses?
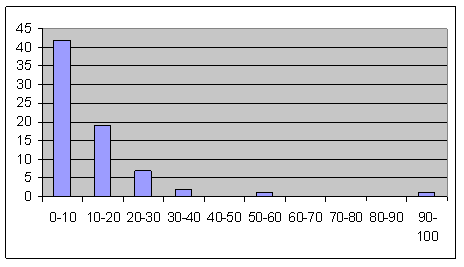
The average was 12.4 (of which two-thirds is 8.3).
While we can show the unique equilibrium in this guessing game is 0, we saw that in the first iteration guesses were wildly off this. This deviation from equilibrium is typical. The game has been run numerous times (see Nagel, 1995; Camerer, 1997). At the Wharton School of Business, the average was 40, as it was among a group of CEOs. With Caltech undergraduates, the average was 30, unusually with 10% at 0 (too smart for their own good). For a group of economics PhDs, the average was 25. In the second iteration, things are always quite different and guesses are drastically lower. Thus, when the game is repeated equilibrium theory does much better.
So, what makes this an economic experiment? There is a clear prediction from economic theory that is tested by having students respond as the agents in a model.
From this game, one can clearly see the advantages of classroom experiments. The experiment is fun for the students to play. When a similar game was played by asking newspaper readers (Financial Times) to send in a guess (Nagel et al., 2002), there were thousands of responses. Even though the experiment is very simple, it generates plenty of discussion amongst the students. By playing the game, they also quickly grasp the concept of equilibrium and its prediction, far more easily than by explanations alone. Moreover, it teaches students to think about whether the models we teach them apply, and to see for themselves when they do or do not. As in this case, they often see both possibilities. As Colin Camerer (1997) puts it, ‘So game theory, which seemed so laughable at first, does predict what people will do with repetition. Again, psychology helps us understand what happens at first, and game theory tells us what will happen eventually as people learn. We need both to understand the entire picture.’
Hints for running this experiment
- Run the first round of the experiment at the end of a lecture. The students have to write their names and a guess onto a piece of paper which you can collect in a box at the end of the lecture. You (or some assistant, for instance a student) can then put the numbers into a spreadsheet and the winners be determined.
- Explain the result at the next lecture and then play another round.
- Instead of showing the results of the first round, one can discuss typical results (e.g., the one above or those in Nagel’s paper). Then play both rounds in one session.
- It is nice to give a prize to the winner such as a book. Freakonomics or the Undercover Economist are suitable prizes which are not very expensive. Prizes should be announced before the experiment. If you have only one prize, let students throw a coin to decide whether the prize goes to the winner of the first or second round.
4. Types of classroom experiments
There are three ways of running classroom experiments: hand run, computerised and homework. For instance, we ran the above guessing game experiment by hand.
A. Hand run experiments
Hand run experiments can be as basic as asking for a simple raise of hands (or electronic polling). One can ask who would co-operate and who would defect in a symmetric prisoners’ dilemma. There are also simple experiments such as the previously discussed guessing game or the auctioning of a £1 coin. Two-by-two games can be played by having slips of paper in two different colours, one for each type of player.
Hand run games can become more sophisticated and require more interaction between the players. One of the first experiments run in a classroom was a hand run experiment by Chamberlin (1948), called the pit market experiment where students act as buyers and sellers (see case 2 below). The pit market experiment can be run with little effort using playing cards. (The pit market is like an old-style commodity exchange, where each commodity is traded around a pit.) The prisoners’ dilemma and public good games can also be run in the classroom using playing cards to cheaply and effectively distribute the pay-offs. More complex trading games can be used in order to illustrate the impact of asymmetric information on market efficiency. For more details see the following links:
- Classroom Experiments & Games (Economics Network theme)
- Case Study: Introducing Classroom Experiments into an Introductory Microeconomics Module (Economics Network).
A more involved hand run experiment is the International Trade Game (see handbook chapter on Simulations, Games and Role-play); although not based upon a research experiment, it is very useful at conveying a wide area of fundamental economic concepts.
Advantages
Hand run experiments have several advantages. Some are suitable for large lectures; others can take just a few minutes to run. Hand run experiments are often an excellent way to engage students, since the interaction is face to face (as in the trade game or the pit market) and some can involve physical activity (as with flower pot/tennis ball http://www.bized.co.uk/educators/16-19/economics/firms/lesson/dimreturns.htm or https://www.economicsnetwork.ac.uk/showcase/hedges_tennis).
Disadvantages
There may be reasons why you may want to use forms of experiments other than hand run experiments. One difficulty is that certain hand run experiments may require careful preparation, including room structure. They also may require assistants, volunteers or another lecturer. This requires careful coordination beforehand. From our own experience it is quite dangerous to try to ‘wing-it’. During one experiment in a class of 300, we were not organised about how to tabulate the results. Both of us had intended only to sample the data, but had not agreed how to do so. We were later told that in the middle of the class students were taking bets on which one of us would slug the other first.
Hand run experiments may require several practices before the lecturer gets the procedure down to a fine art. This may cause a variation in the student experience. There are also a limited number of rounds for which one can run within a lecture or session. Data collection and entry into an Excel spreadsheet can take time and effort. It is quite easy for the data to get lost. When the experiment involves large groups of students, feedback may be delayed for instance until the next lecture. It is also quite easy for students to avoid participating.
Helpful hints for hand-run experiments
- At the beginning of the semester/term, cut simple strips of paper (you may want to use two colours).
- Bring several plastic bags from home to collect answers.
- Give verbal instructions/display question.
- It is often sufficient to sample and evaluate only a few answers. Or one can randomly select some students to participate in one round of the experiment.
- One can display last year’s results rather than wait until the data are evaluated.
- Many experiments can be run using a deck of playing cards (see Holt, 2007).
- Know what you are doing beforehand, particularly when working with assistants.
Case study
B. Computerised experiments
When an experiment requires many rounds and complicated matching schemes it is easiest done on a computer network. A typical example is the Bertrand duopoly game where it is best to use two different types of matching (fixed/random) and/or two different group sizes.
A large selection of computerised experiments is available via Charlie Holt’s Veconlab, Econport and our own FEELE website. Typing any of these keywords into Google will lead you directly to the relevant site. Veconlab offers the most information and help for a beginner. Once this system is familiar, it is easy to switch to our site which is deliberately of a similar design. Econport offers the best market experiment software, in particular for some experiments on financial markets. It is well-documented and easy to understand. How well it works in your computer lab depends on the ingenuity of your university IT group. The more complex and convoluted their firewall system, the less likely it is that the Java applets Econport uses will work and communicate without problems. This system has to be tested in every room where you intend to use it, preferably by your computing officers and IT services.
Advantages
Many of the most popular classroom experiments are offered via the Internet for free. Apart from this, the big advantage of computerised experiments is their availability and the ease at which beginners can get started. The student experience tends to be uniform. The results are available immediately and can easily be distributed to students for evaluation. In many cases, there are tools provided for simple analysis of the results. A large number of rounds can be run as well as several treatments. An experienced instructor or teaching assistant can handle a computer classroom alone, although it is easier, particularly if there are more than ten students, if one instructor concentrates on the software and another on the students.
Disadvantages
One main disadvantage is that the experiments are standardised. While there are some parameters a lecturer can change, there is not the broad opportunity for drastic innovation that a hand run experiment offers.
A second problem is the requirement to have a special computer room (and it helps to have a projection screen for the instructor’s computer). There is the usual hassle of reserving the room and organising the students to meet there. On a practical level, there is a limit to how many students can fit in the room. When there is a large class, you may have to split it up into several groups. This creates an additional teaching burden. The alternative is to use tutorials, which may have a higher opportunity cost.
Another problem is that in many cases the experiment tends to run as fast as the slowest student. You constantly have to control the monitor program to see how the experiment is progressing and may also have to check the screens of individual students. Students often check their email or Facebook accounts and therefore the experiment becomes stuck. If the experiment runs too slowly, boredom may set in, creating a free-rider problem for students paying attention. Once things are started and running smoothly, there is also the danger that the instructors may check their email as well and not realise that there is a delay. Luckily there is now a KIOSK program that keeps the computer locked in the experiment (see the hints).
Finally, there is a risk of technical problems, such as software bugs, network failure and IT-related problems. This is particularly true for experiments using technically more advanced software. However, such problems have only rarely occurred with our software and that of Veconlab, since they require only a standard web browser.
Helpful hints for computerised experiments
- Place two students per computer to make decisions jointly. The students will discuss their options and this will typically lead to better decisions; they will ‘catch on’ quicker and have a deeper learning experience. It also helps foreign students who have difficulties with the oral or written instructions. Moreover, the amount of web surfing, etc. will be reduced. It also eliminates the danger of holding up the whole class with a single toilet break.
- Give instructions by email or handouts beforehand. Again, this helps non-English speakers and students with reading difficulties, in particular dyslexic students. Getting students to read and understand the instructions takes substantial time out of the experiment.
- Let students in different sessions play the same treatments in a similar order. Otherwise, they do not have the same learning experience.
- Try setting up and playing the experiment beforehand. One can do this by setting up a smaller number of players in different web browsers on a single computer’s desktop (sometimes one needs different browsers rather than different tabs within a browser).This would help you not only decide if you like the experiment, but help decide what treatments and parameters to run. It is also important to have you see what the students see, for discussion and questions.
- Try configuring the experiment beforehand. Doing so saves time and reduces the number of errors or restarts. There is, however, a limit to what is possible, since many experiments need the full number of participants (or terminals) to be logged in before the experiment can be started. Luckily, both Veconlab and our website are currently enhancing the possibilities to change the number of participants on the spot.
- Prevent email checks by students. The terminals can be run in KIOSK mode which prevents students from using the computer for anything but the experiment. Via our FEELE website you can start the KIOSK program to either run our experiments or those on Veconlab (simply Google ‘FEELE kiosk’; this requires Internet Explorer).
- Distribute handouts explaining how to log in; reduces 'finger trouble' and saves time.
- Number the handouts beforehand and distribute one per computer; avoids headcount errors when configuring subject numbers.
Case studies
- Case 3: The hold-up problem (computerised)
- Case 4: Price competition (computerised)
- Case 5: Bank runs (computerised)
C. Homework experiments
Homework experiments are simply classroom experiments that are meant to be played at home instead of during class hours. The most basic is a simple one question and answer format with feedback and summary of the results discussed in class. There is an elegant website by Ariel Rubinstein that is designed especially for this purpose. A slightly more complicated homework experiment is to run a more advanced individual choice experiment with some immediate feedback (for instance we have a computerised Monty Hall problem that is played several times). Finally, it is possible to have students play against a fictitious player such as a robot playing a particular strategy or against prior human players. The first example we know of using this option is Charlie Holt with his traveller’s dilemma experiment available on Veconlab. We now offer for most of our experiments ‘quick log-in’ versions where you play against a past group of participants.
Another innovation by Charlie Holt is running the standard multi-player experiments by having students log on from home at a specific time in the evening. There are also experiments (such as prediction markets) that can be run over several weeks. In fact, such homework experiments (such as the Iowa political stock market) predate the web.
Advantages
The main advantage of a homework experiment is that it can save lecture and tutorial time. There is very little hassle and one does not have to worry about time limits. They provide great flexibility to both students and lecturers.
Disadvantages
Overall, the lecturer has little control with homework experiments. There is no guarantee the student is the one playing the game. If the experiment requires interaction among subjects, there is no means to stop collusion. If it is an individual choice experiment, one student can advise another. Without additional incentives the overall participation rate can be low. Though for some experiments we have had the opposite problem of some students playing the game several times in order to beat the previous performance. Currently there is still a limited variety of home-run experiments which every student can do by him or herself. One can invest the extra co-ordination of running group experiments at a specific time. Even with these one needs to keep the group size small so one player does not hold the rest up (toilet breaks are problematic here).
Helpful hints for homework experiments
- Use some sort of incentive for participation.
Case study
5. Integration into a module
In using experiments there are many challenges that must be overcome. These are for lecturers, students and the modules overall. Lecturers have a limited amount of time in lectures. Students have limited time too (both inside and outside the classroom). Proper assessment and motivation of students can be a challenge as well. Here we try to answer a number of issues that need to be considered when implementing experiments.
- Which particular experiments to use?
- Which type of experiments to use (homework, hand run, computerised)?
- How many experiments to use?
- How to count experiments toward the final mark?
- How to base exam questions on experiments?
- General hints
Two brief case studies on modules using experiments and their student evaluations
Case 1: Intermediate Microeconomics (100 students)
Intermediate Microeconomics in Exeter, part 2 (100 students, lectures, surgeries and experimental sessions). We ran simple 2x2 games and auction games within the lecture. Students had to do 8 out of 6 computerised assignments (Wiley Plus), 3 homework experiments and 6 experimental sessions, in order to get 10 out of 100 marks for the module. Apart from that, participation was voluntary, to allow for different learning styles. The incentive was for participating, not for getting it ‘right’. (We intend in the future, however, to have for each experimental session a short questionnaire with simple questions of understanding.) It was not expected that every student would do every session. Each experimental session was run twice to allow many students to participate. Participation in experimental sessions was increasing over the year. The lectures would frequently refer back to the experiments, discuss the results and compare them with the theoretical analysis. The module was surprisingly successful in the students’ evaluations, with an average above 4 out of 5 on the goodness index, and the highest score for the question on how useful the experiments were for the module. The response rate was higher than for many other comparable modules (40%). Exam results were similar to those in previous years, however we did not make a systematic evaluation.
Case 2: Third Year Option (30–40 students)
Another type of module is where each lecture is designed around experiments. Each week there is an experiment followed by a lecture based upon the experiment. This has worked successfully in both a Corporate Strategy course for executives (10–15 students) and a third-year course (30–40 students). The third-year course was meant for economics students that had taken microeconomics and had a diverse number of topics. There were experiments on markets and market structure: Bertrand Competition, Bertrand Complements, Vertical Markets, and Double Auction with Taxes. Experiments on multi-player simultaneous choice games: Bank Runs, and Network Externalities. Two-player sequential games: Hold-Up Problem, Team Draft, Ultimatum Game, and Signalling. Also there were several individual choice experiments: Price Discrimination, Lemons Game, Monty Hall, and Search.
For the third year module we have detailed student evaluations for 14 classroom experiments. Overall, students found they learned from experiments 3.8 on a 1–5 scale. They rated the fun 4.05. This order is consistent with 12 out of the 14. When there were technical difficulties in running the experiments, it significantly hurt the ratings in both categories. In addition, homework experiments (all individual choice) were less popular. The most popular experiment by average rank of learning and fun was the Bertrand Competition experiment (run on FEELE) which was first in fun and second in learning, following by Team Draft (FEELE), Ultimatum game (Veconlab), Signalling (Veconlab), and Bank Runs (FEELE). Another noteworthy experiment was a tax incidence experiment using Econport’s Marketlink double-auction software. It had an average rating of 4.41 out of 5 for fun, even though students rated the learning only average.
Which particular experiments to use?
Here are some recommendations:
Microeconomics is the module with the most experiments developed for it, so it is fairly easy to fill.
Macro: Denise Hazlett’s website has several experiments. In addition, for a large class, Currency Attack (available on the FEELE site) works well.
Money and Banking: There is the bank-run experiment described here as well as a computerised Kiyotaki-Wright experiment based upon an experiment by Denise Hazlett.
Finance: The Holt bubble experiment is recommended. The double auction on Econport is able to impress many, in particular the version for an asset market. During the opening of a new finance centre at Exeter we demonstrated this software and many of those in industry were hooked. There are also some experiments that can be used to introduce behavioural finance. For one, the Monty Hall experiment shows how poorly people do as individuals, but things look quite different when the game is placed in a market setting (one can refer to a Journal of Finance article on this). An experiment that proved popular with the students is the Being Warren Buffett experiment. This was developed at Wharton and we have a computerised version of it on FEELE.
Game Theory and Decision Theory: The Rubinstein website is an ideal source for homework experiments on both topics. Veconlab offers some excellent experiments for game theory, but also for Bayesian learning. Team draft and the Hold up experiment on the FEELE site are good introductions to backward induction. Quick and simple hand run experiments, e.g. many of the questions used by Kahneman and Tversky and simple experiments on one-shot 2*2 games. For repeated games one can use a repeated prisoners’ dilemma or one can play a repeated Cournot duopoly using Veconlab.
Industrial economics: Again, this is a module for which plenty of experiments exist, for instance on Veconlab or FEELE.
Introductory economics: The size of the lecture is crucial. The guessing game, a simple insurance game (see the classroom experiments site on Wikiversity), and a hand-run public good game can be done with little effort. If at all possible one should run a double auction or pit market experiment to discuss market equilibrium. The student activity on decreasing marginal returns using tennis balls or plastic flower pots is highly recommended and can be done with a sample of students even in big lecture halls. A colleague of ours just ran (with some help from other staff) the international trade game (see Sutcliffe’s handbook chapter (2002) on Simulations, Games and Role-play) in a group of 100 students.
Which type of experiments to use (homework, hand run, computerised)?
Type guidelines
- Large lectures (>100 with no tutorials): Use short hand run or homework experiments. It is possible to be more sophisticated with wireless technology.
- Medium lectures (40<#<100): Make use of computerised experiments or (more labour intensive, but also more fun) hand run longer experiments in tutorials.
- Small lectures (<40): You can use computerised experiments in place of lectures if you have access to a computer room.
How many experiments to use?
There is no minimum or maximum. We have had classes that have run an experiment a week and particular lectures (like one on game theory) that run several short experiments in a single lecture. In microeconomics we ran weekly experimental sessions on a voluntary basis. We had a regular following, but also people who never came. It is important for the students not to feel overloaded and to experience a variety of teaching approaches. We think that one, sometimes very short, sometimes longer, experiment per topic is ideal.
How to count experiments toward the final mark?
We found the most successful strategy for employing experiments has been to give marks for participation, not success, in an experiment. Participation was optional and a potential replacement for turning in homework. Also, we have successfully required lab reports that consist of explaining students’ strategy in the experiment, analysing experimental results and answering a few simple questions (short answer/multiple choice) on problems relating to the experiment. Implementing a computerised version of such a lab report is quite simple using the Veconlab's surveys.
Dickie (2006) confirmed Emerson and Taylor’s findings that experiments improved TUCE scores: however, they found that this benefit disappears if one bases credit on performance. We guess that this may be due to at least a perceived randomness in performance, although we have noticed that the same students do well across several experiments throughout the term. In any case, perceived randomness can not only hurt evaluations, but could raise the alarm of a teaching committee. Giving prizes for performance seems to draw no criticisms. There does not seem to be an objection to a lottery for a prize just a lottery for a grade.
We feel it is useful to have exam questions based upon the experiments: more the carrot than the stick. This leads us to the next point.
How to base exam questions on experiments?
There are studies showing that experiments helped to improve test scores both on the TUCE (general knowledge) test and in standard exams. Still, the students are unaware of this, and there is always room to tie things together more closely. Moreover, common sense tells us that for a quantitative exam, having a tutorial based upon mock questions similar to the exam is liable to boost scores more than running an experiment with only a tangential connection. The first year we ran experiments, we found that a handful of students thought that the experiments were at the expense of valuable tutorial sessions, and were being run for the benefit of the lecturers. Clearly, tying the exam more closely to the experiments should help.
In many cases, experiments can help students learn a particular exam question. For instance, the network externality experiment on the FEELE site is specifically based on a chapter in Hal Varian’s Intermediate Microeconomics book. More generally, the signalling experiment on Veconlab is extremely helpful in teaching signalling to undergraduates. We believe this may have the most value added, in that without experiments we found it difficult to teach signalling. Likewise, the price discrimination experiment is based upon a style of test question, rather than the other way around.
For other cases, the experiments may help general understanding, rather than learning a particular algebraic manipulation. With Cournot duopoly, an experiment may help students grasp simple comparative statics, while algebraic manipulations are subject to sign errors.
Naturally, any exam question can be used as a homework question, but one can also have homework questions based upon analysing the data from an experiment. The FEELE site has an option to create a link of the results in both numeric and graphic form for the students (via the button of ‘View Results (Subject)’). This makes the task fairly easy. Since the data from the experiment are available, they can be used to develop exam questions: for instance, to what extent does the experimental data fit the predictions of the theory?
General hints
- Usually do experiments before covering the material in the course.
- Let students participate in preparation, execution and evaluation (especially in an experimental class).
- Relate some exam questions to experiments.
- Do not be too obsessed with preserving a research environment.
- Use two students per computer to induce discussion and reflection.
6. Resources
There are many resources available via the web. A good starting point is a Wikiversity site that we started called ‘economic classroom experiments’. To get there just google ‘economic classroom experiments’. This describes how to run many classroom experiments and has links to all the other resources mentioned here. You are invited to help to develop this website. If you find any links missing, please add them. If you can report on a teaching experiment you conducted, you are cordially invited to make your report available via this website. The site is among a selected group of Wikiversity Featured Projects.
If you wish to run a computerised classroom experiment, the easiest site to get started is Veconlab, developed by Charlie Holt. This site consists of almost all the basic economic classroom experiments. Holt has also written a textbook Markets, Games, and Strategic Behavior (2007) that has a chapter for many of the games available on this site. The site is very reliable and works anywhere you have a web browser.
Another site, FEELE, is one which we developed as part of an FDTL5 grant. It mimics Holt’s site and is meant to be a complement. Since we offer KIOSK you may also want to start Veconlab experiments via our website.
Econport has a beautifully written version of the double auction (Vernon Smith's basic demand and supply curve experiment) with extensions to financial markets. The site also offers a very useful online handbook for micro economics and much more.
For a game theory or microeconomics course, one should take a close look at Ariel Rubinstein’s site. He makes it fairly easy to design the module as a whole and track student responses. All the experiments are homework experiments on decision and game theory and are played via the web so do not take up lecture time.
Denise Hazlett has details of six of her macroeconomic experiments via the website http://people.whitman.edu/~hazlett/econ/.
Last but not least, there are plenty of resources and links available on the classroom experiments page of the Economics Network.
7. Conclusions
We hope the above has whetted your appetite to start using economic classroom experiments as a tool for active student learning. We have discussed advantages and disadvantages and given a number of concrete hints. We would like to encourage you to try them even if you are in general somewhat sceptical of experimental research. See for yourself how a simple experiment can demonstrate to students that economics ‘works’. Discuss with your students what can and cannot be inferred from the experiments. You may at first decide to adapt only a small portion of your module in order to try out a single classroom experiment or a few short homework exercises. Even this, we think, is time well spent.
We realise that a major cost to the instructor of using experiments is the uncertainty of how they will work and the fear that it will take significant effort to introduce them. It may seem easier to just keep using the same old teaching materials. We hope that the concrete examples in this handbook chapter will reduce the perceived cost and encourage you to get started.
If we have managed to convince you that the benefits outweigh the costs, then please contact us with any questions, suggestions or simply to report on your experience. Good luck!
8. References
Balkenborg, D. G., Kaplan T.R. and Miller, T.J. (2009) Teaching Bank Runs with Classroom Experiments. Discussion paper, Department of Economics, Exeter 2009, forthcoming.
Balkenborg, D. G., Kaplan T.R. and Miller, T. J. (2009) A simple economic teaching experiment on the hold-up problem. Discussion paper, Department of Economics, Exeter, forthcoming. https://doi.org/10.1080/00220485.2012.714310
Ball, S. B., Eckel, C. and Rojas, C. (2006) ‘Technology Improves Learning in Large Principles of Economics Classes: Using Our WITS’, American Economic Review, 96(2), 442–446. https://doi.org/10.1257/000282806777212215
Beckman, S. R. (2003) ‘Cournot and Bertrand Games’, Journal of Economic Education, 34(1), 27–35. https://www.jstor.org/stable/30042521
Bergstrom, T. C. and Miller, J. H. (2000) Experiments with Economic Principles, MacGraw Hill: New York, 2nd ed.
Camerer, C. (1997) ‘Taxi Drivers and Beauty Contests’. Engineering and Science, No. 1, 10–19
Chamberlin, E. H. (1948) ‘An Experimental Imperfect Market’, Journal of Political Economy, 56, 95–108. https://doi.org/10.1086/256654
Diamond, D. W. and Dybvig, P. H. (1983) ‘Bank Runs, Deposit Insurance, and Liquidity’, Journal of Political Economy, v91, 401–419. https://www.jstor.org/stable/1837095
Dickie, M. (2006) ‘Do Classroom Experiments Increase Learning in Introductory Microeconomics?’, Journal of Economic Education, 37(3), 267–288. https://doi.org/10.3200/JECE.37.3.267-288
Durham, Y., McKinnon T. and Schulman, C. (2007) ‘Classroom Experiments: Not Just Fun and Games’, Economic Inquiry, 45(1), 162–178. https://doi.org/10.1111/j.1465-7295.2006.00003.x
Emerson, T.L.N. and Taylor, B.A. (2004) ‘Comparing Student Achievement across Experimental and Lecture-Oriented Sections of a Principles of Microeconomics Course’, Southern Economic Journal, 70(3), 672–693. https://doi.org/10.1002/j.2325-8012.2004.tb00596.x
Hart, O. (1995) ‘Firms, contracts, and financial structure’, Clarendon Lectures in Economics, Oxford and New York: Oxford University Press, Clarendon Press.
Holt, C.A. (1996) ‘Classroom Games: Trading in the Pit’, Journal of Economic Perspectives, 10:1, 193–203. https://doi.org/10.1257/jep.10.1.193
Holt, C.A. (1999) ‘Teaching Economics with Classroom Experiments: A Symposium’, Southern Economic Journal, 65(3), January 1999, 603–610. https://doi.org/10.2307/1060819
Holt, C.A. (2007) Markets, Games, and Strategic Behavior, New York: Pearson Addison Wesley.
Kaplan, T.R. and Wettstein, D. (2000) ‘The Possibility of Mixed-Strategy Equilibria with Constant-Returns-To-Scale Technology under Bertrand Competition’, Spanish Economic Review, 2(1), 65–71. https://doi.org/10.1007/s101080050018
Kolb, D.A. (1985) LSI Learning-Style Inventory, McBer & Company, Training Resources Group, 116 Huntington Avenue, Boston, MA, 02116.
Krugman, P. (2000) ‘Microsoft: What Next?’ New York Times, 26 April.
Nagel, R. (1995) ‘Unraveling in Guessing Games: An Experimental Study’, American Economic Review, 85, 1313–1326. https://www.jstor.org/stable/2950991
Ruffle, B.J. (2003) ‘Competitive Equilibrium and Classroom Pit Markets’, Journal of Economic Education, 34:2, 123–137. https://doi.org/10.1080/00220480309595207
Ruffle, B.J. (2005) ‘Tax and subsidy incidence equivalence theories: experimental evidence from competitive markets’, Journal of Public Economics, 89, 1519–1542. https://doi.org/10.1016/j.jpubeco.2004.04.009
Sutcliffe, M. (2002) ‘Simulations, games and role-play’, Economics Network handbook chapter. https://doi.org/10.53593/n2913a

