Understanding the construction and interpretation of forecast evaluation statistics using computer-based tutorial exercises

The construction and interpretation of forecast evaluation statistics are central components of any course on economic forecasting. Without an understanding of these issues, students will neither be able to evaluate the properties of a set of forecasts, nor will they be able to assess the relative merits of alternative sets of forecasts. In recent years, I have covered the use of forecast evaluation statistics as the initial topic on a Level-M course on economic forecasting. In addition to presenting this material in a standard lecture setting, I have also employed computer-based tutorial exercises to reinforce the learning process.

I have found the introduction of computer-based exercises using Excel to be extremely beneficial for two principal reasons. Firstly, the actual process of calculating alternative forecast evaluation statistics directly from a series of interest and a set of forecasts of it, develops a clear understanding of the construction of the alternative statistics available. Secondly, via the use of carefully selected hypothetical data and forecasts, the properties of alternative forecast evaluation statistics can be highlighted. In particular, the specific information provided by alternative statistics can be clearly demonstrated. This reinforces the message that no forecast evaluation statistic is redundant as each has information to impart. This is an important issue as textbooks tend to adopt a hierarchical presentation of forecast evaluation statistics which suggests that basic statistics can be neglected in favour of more sophisticated alternatives. However, this is clearly not the case. For example, while Theil's U-statistics have a number of attractive properties, they do not provide information on forecasting bias which is captured by the mean error, the most basic of all forecast evaluation statistics. Using computer-based exercises, the complementary information provided by alternative forecast evaluation statistics can be demonstrated and it can be made clear that a full range of statistics needs to be considered for the complete analysis of a series of forecasts.

The forecast evaluation statistics considered in my coverage of economic forecasting are: the mean error (ME), the mean squared error (MSE), the mean absolute error (MAE), the mean percentage error (MPE), the mean absolute percentage error (MAPE), and Theil's U-statistics. Theil's U-statistic is presented in both of its specifications, these being labelled U₁ and U₂ respectively. Denoting a series of interest as y_t and a forecast of it as f_t, the resulting forecast error is given as e_t = y_t - f_t, for t = 1,...,T. Using this notation, the (fairly standard) set of forecast evaluation statistics considered can be presented as below:

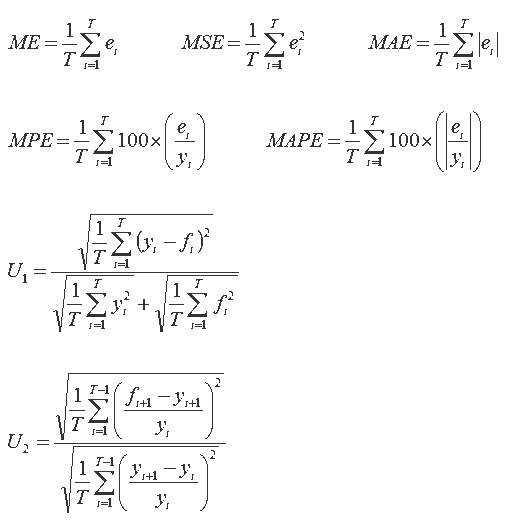
The linked Excel file provides an example of the tutorial exercises I have undertaken. The file contains two completed spreadsheets providing calculated values of the above statistics. In the first spreadsheet (Example 1), the variable of interest (y) is accompanied by two sets of forecasts of it (F1 and F2). It can be seen that F1 is a no-change forecast, or nave forecast as it is referred to in forecasting textbooks, in which forecast of y for period t+1 is simply its observed value in period t. I include this simple forecast as it provides a benchmark against which other forecasts and forecasting methods can be compared. The second spreadsheet (Example 2), presents a similar analysis with the variable of interest and the two sets of forecasts it denoted as x, F3 and F4. Again, the first of the forecasts (F3) is a no-change forecast. Note that when distributed to students, the spreadsheets contain the series of interest and forecasts only.

Turning to the results in the spreadsheets, it can be seen that due to the nature of the chosen data series and forecasts, the information provided by the alternative forecast evaluation statistics is apparent. Amongst the various issues demonstrated are the following:

• A low value of the ME may conceal forecasting inaccuracy due to the offsetting effect of large positive and negative forecast errors. This is apparent when comparing F1 with F2, and F3 with F4. In both cases the former nave forecast (F1,F3) dominates its rival (F2,F4) with a zero value obtained for the ME. However, despite the unbiasedness of the forecasts, their inaccuracy becomes apparent from inspection of subsequent forecast evaluation statistics.
• The MSE and MAE may overcome the 'cancellation of positive and negative errors' limitation of the ME, but they fail to provide information on forecasting accuracy relative to the scale of the series examined. This issue is apparent from comparison of F1 and F3. On the basis of the MAE and MSE, F1 appears to provide more accurate forecasts than F3. However, these statistics do not take account of the fact that the observed values of the 'x' series forecast by F3 are greater than the values of the 'y' series forecast by F1. Consideration of the scaled measures (MPE, MAPE, U₁) show F3 to be preferred to F1 once the greater size of the series forecast is allowed for. That is, while the errors of F3 are greater than those of F1, they are smaller relative to the scale of the series of interest. A similar story results from the comparison of F2 and F4.
• The MSE places a greater penalty on large forecast errors than the MAE. To illustrate this, consider F2 and F4. In both cases, the forecasts errors are non-negative and sum to -10. As a result, F2 and F4 return the same calculated values for ME and MAE. However, while the errors of F2 are more evenly distributed, F4 generates a relatively large error (-7) for one period. Consequently, the calculated value of the MSE is much larger for F4 than F2 (7.43 compared to 2.57), despite the noted equality of the ME and MAE under both sets of forecasts.
• The more accurate the forecasts, the lower the value of the U₁ statistic. The U₁ statistic is bounded between 0 and 1, with values closer to 0 indicating greater forecasting accuracy. On the basis of the above arguments, F4 represents the 'best' set of forecasts of the four considered. This is illustrated by the calculated U₁ statistic for F4 being the lowest reported.
• The U₂ statistic will take the value 1 under the nave forecasting method. Values less than 1 indicate greater forecasting accuracy than the nave forecasting method, values greater than 1 indicate the opposite. When considering the statistics for F1 and F3, it can be seen that while they return differ values for the MSE, MAE, MPE and MAPE, both forecasts return a value of 1 for the U₂ statistic as both are nave forecasts.
• Even the simplest forecast evaluation statistic provides useful information. While the more sophisticated forecast evaluation statistics provide information on the properties of the alternative forecasts, the mean error provides useful information on the bias of the actual forecast errors. For example, the bias of the F2 and F4 sets of forecasts can be drawn from the ME while it remains hidden in all other statistics apart from the MPE where it is depicted in a scaled form.

The above Excel file shows how simple exercises with hypothetical series of data and forecasts can reinforce understanding of the construction, properties and interpretation of alternative forecast evaluation statistics. While the spreadsheets are presented with short runs of data in the interests of simplicity, they can be easily extended to analyse longer runs of data or real-world forecasts from alternative forecasting methods such as exponential smoothing or econometric modelling.