Writing and using computer-aided assessment (CAA) in mathematics for economics first years
Martin Greenhow
Department of Mathematical Sciences, Brunel University
Published May 2012
Links updated May 2022
Computer-aided assessment (CAA) now forms a significant part of many students’ experience of higher education, especially for subjects with a significant mathematical/analytical content. Several mature technologies now exist that can reach beyond their intended audience and discipline, meaning that CAA looks likely to be increasingly pervasive, at school or for in-service training. Such assessment should not simply grade students, but should promote learning, which means that effective questions will need to be based on sound pedagogic principles.
Greenhow and Zaczek (2011) discuss the processes of writing objective questions and exploiting the computer medium: we note here their main points. Given its immediacy, it is clearly essential to write clear and full feedback. Moreover, questions should also include random parameters, so that many thousands or millions of realisations are generated by underlying encoded algorithms. The randoms are carried through to all parts of the question (stem, key, distracters and feedback) and equations (via MathML) and accurate diagrams (via SVG), so that that all element of the question are generated at runtime. These parameters usually generate different numbers, but can also generate random words or question scenarios.
The question author is then required to encapsulate the algebraic and pedagogic content of all questions of a certain class, a process quite unlike the setting of paper-based tests. This usually involves reverse engineering the question from the answer’s requirement to have certain characteristics e.g. whole numbers, easy fractions etc. The pros and cons of various question types also need consideration, especially the merits of responsive numerical or responsive word input questions where mal-rules can be programmed ‘behind the scenes’ to produce predictable wrong answers that, if input by the student, will trigger bespoke feedback.
Of course, even sound and robust CAA will only be effective if students engage with it. A practical strategy for enforcing this is to make a genuine exam pass mandatory rather than an overall pass with CAA marks included. This forces students to focus on the learning process right to the end of the module. Even with engaged students, the efficacy of CAA needs to be examined, both in terms of their perception of the tests (very positive but not presented here) and the actuality of their learning, see below. Although the limitations of CAA are readily acknowledged, the results below indicate a strong case for including CAA within the overall (blended) assessment strategy.
Most of the 2000 questions (each producing thousands of realisations) that form the above CAA system are now available via a new (and free) web application Maths E.G. at: https://www.mathcentre.ac.uk:8081/mathseg/ (student interface – see figures 1 & 2) and https://www.mathcentre.ac.uk:8081/mathsegteacher/ (teacher interface).
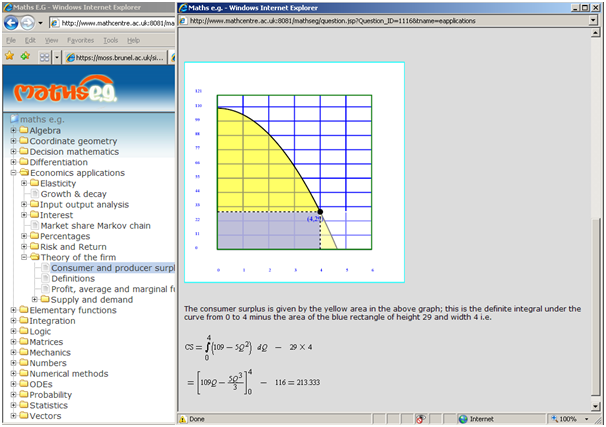
Figure 1 The Maths E.G. student interface, showing the topic tree comprising circa 2000 questions and a question’s feedback screen, selected from Economics. Here the numbers are randomised and used in the MathML equations and in the SVG diagram; both are created on the fly when the question is loaded (neither is a fixed graphic). The question was developed under the Metal Project: https://www.metalproject.co.uk/
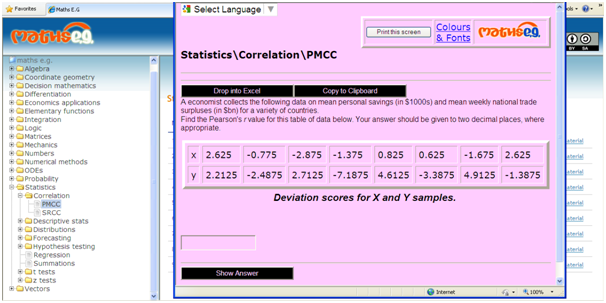
Figure 2 The maths e.g. student interface, showing the topic tree and a (randomised) question selected from Statistics showing Excel and Clipboard buttons and Google’s translator into circa 50 languages. The colour scheme/font size are under the student’s control which is probably useful for partially-sighted or dyslexic students. The question and the interface was developed under the DeSTRESS Project: https://economicsnetwork.ac.uk/statistics
Case study: EC1005 Mathematics for Economics
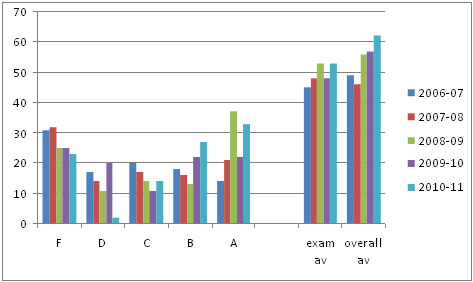
In 2006-07 the Department of Mathematical Sciences at Brunel University was asked by our Economics Department to share the teaching of their first year mathematics and statistics/research methods modules (EC1005 & EC1006). Given that I was writing the CAA material for the FDTL5 Metal Project, I welcomed the chance to teach the group without A-level mathematics (typically about half the cohort of about 340 students aged 18-20 years, 55% male) since I anticipated using the CAA to replace the two class tests. In fact this did not happen until 2008-09 (for the both cohorts); in addition to saving me about 8 solid days marking, the exam and overall performance of the students then increased substantially: see figure 3. During these three years the performance of the two groups (with/without A level) was indistinguishable at the end of the year, and it was felt that the weaker students benefitted relatively more from the CAA.
In 2009-10, I took over the entire cohort and the admissions policy changed to require at least AS level mathematics. In fact, about half of the cohort had the full A-level at grade B or above, and the qualifications for this year (2010-11) comprise grades A*(3%), A(12%), B(50%), C(21%), D(4%) with the rest having AS grades A(3%), B(4%) and C(3%). It is gratifying that very few students that took AS level mathematics did not continue to the full A-level. Given the enhanced mathematical preparedness of the students since 2009-10, the low exam average was somewhat disappointing. It can be explained by the fact that I set the exam for the first time and overestimated the speed with which students could do the questions (corrected in 2010/11, although the exam is still undoubtedly harder than those set in 2006/7 & 2007/8).
The overall average slightly increased, but some 70 students had to resit the examination in September 2010 since a genuine pass in the exam component was introduced as a module requirement (in addition to the exam being weighted at 70%). Of the 2009/10 resitters about 50 passed. Results for 2010/11 are encouraging across all grades and of 55 resitters, 50 passed (helped no doubt by the continued use of the CAA over the summer for revision purposes).
Figure 3 Year-on-year overall grades (% of students), and exam and overall averages (% marks).
Reference
Greenhow M. and Zaczek K.(2011) Embedding computer-aided assessment of mathematics and statistics for first year economics students Proc ICTMT10 Conf, Portsmouth http://ictmt10.org/ (accessed 17/2/12)

