Dr. Charles Smith
Swansea School of Education, Swansea Metropolitan University, University of Wales
smithcejk at hotmail.com Published April 2006
Introductory notes
These notes are brief, as the accompanying Powerpoint Presentation is self-contained and should be self-explanatory.
© Dr. Charles Smith, 2006
The author asserts and reserves all rights.
However, this resource can be freely copied, adapted, and used by teachers under the following conditions:
- The source is acknowledged in your presentation:
(cite as: Smith, C. (2006), Building-Blocks of Understanding, in ‘Reflections on Teaching’, www.economicsnetwork.ac.uk/showcase/classroom); - In return for suspending copyright, the author would be grateful for the following feedback from users:
- Your name, institution, e-mail address
- Date of use of resource
- Type and level of class
- Any amendments incorporated (you could attach a copy of your presentation)
- A brief evaluation of the usefulness of this resource
Please e-mail to: charles.smith@smu.ac.uk
It is hoped to use feedback as a basis for a future study; therefore please state if you would prefer your feedback to be quoted anonymously. Thanks.
Introduction
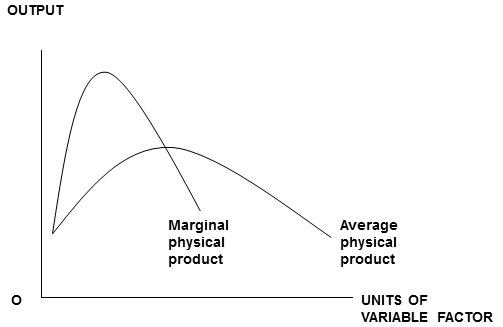
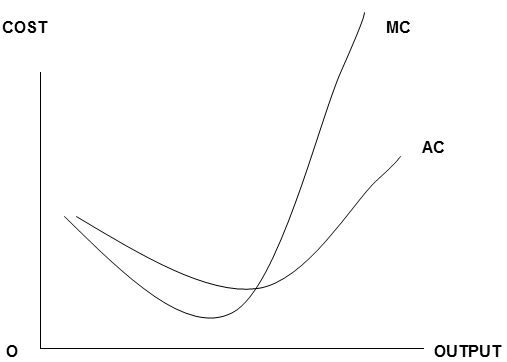
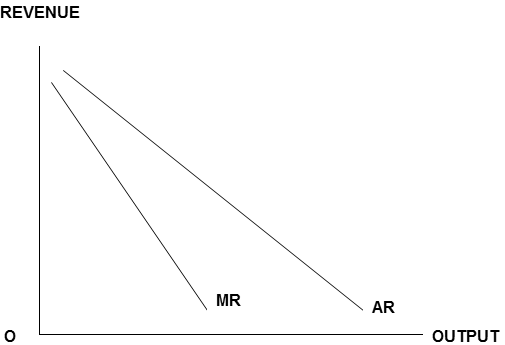
Before embarking on study of business economics or the theory of the firm, students need a thorough grasp of the differences and relationships between average and marginal values.
This resource enables students to investigate these differences and relationships in an accessible and tactile way.
Thus, an aspect of economics which students typically find very abstract, theoretical and difficult, becomes practical, kinesthetic, and easier to understand.
Methodology
Equipment Required
- Plastic building blocks, e.g. the LEGO ® brand
- Squared paper
- (Optional) Microsoft Excel ® spreadsheet
Step 1
- Split your class into groups of 3 or 4 students per table
- Put plenty of blocks on each table
Step 2
Ask each group to make towers containing different (random) numbers of blocks

Step 3
- Place a 'base' on the table.
- Students are going to add towers to the base in ascending order of height.
Step 4
This is tower no. 1; its height is 2 blocks. The average height of towers on the base is 2/1 = 2 blocks per tower. The marginal height (blocks added to the base by the last tower) is 2.
Step 5
Tower number 2 is added to the base, and the corresponding numbers inserted in the table. Two important points arise here. Firstly: marginal height can be calculated in two ways: 1. the no. of blocks in the latest tower on the base; 2. (total height) minus (previous total height)
The second point is that average height (arithmetic mean) is less 'real' than marginal height. There is no tower on the base with 3.5 blocks; there is one with 5 blocks.
Steps 6-8
Continue by adding the next towers and completing the table

| a | b | c | d | e |
|---|---|---|---|---|
| Tower number | Height of this tower (in blocks) | Total height so far | Average height (blocks per tower) | Marginal height (in blocks) |
| 1 | 2 | 2 | 2.0 | 2 |
| 2 | 5 | 7 | 3.5 | 5 |
| 3 | 7 | 14 | 4.6 | 7 |
| 4 | 8 | 22 | 5.5 | 8 |
| 5 | 9 | 31 | 6.2 | 9 |
Investigations
Students can now use this table to draw a graph on squared paper showing average height and marginal height on the Y axis, and no. of towers on the X axis.
Then they can experiment with different sequences of towers, and plot graphs to investigate relationships between average values (AV) and marginal values (MV).
They can then try to derive a list of 'rules' governing AV and MV.
Rule 1
Where AV is rising, MV is above AV

Rule 2
Where AV is falling, MV is below AV

Rule 3
It follows logically from Rules 2 and 1 that as it ascends, the MV graph must pass through the minimum point of the AV graph. So if AV falls and then rises the graphs will look like this...

NOTE: Eagle-eyed students might notice that in this graph, the MV line does notquite pass through the minimum point of AV. This is because the computer has plotted a straight line graph instead of a smooth curve. You can reassure students that Rule 3 is quite correct mathematically.
Rule 4
It follows logically from Rules 1 and 2 that as it descends, the MV graph must pass through the maximum point of the AV graph. So if AV rises and then falls the graphs will look like this...

Rule 5
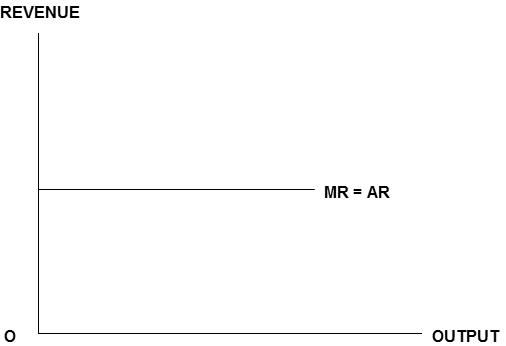
If AV is constant, MV will also be constant, and AV = MV

Students could experiment with AV and MV values using the following spreadsheets, which have suitable formulae already inserted. Students need only add tower heights to column 'b' and the formulae will do the rest. I have 'locked' the first five (if you wish, they can be unlocked using password 'smith'); the sixth is not password-protected, and is intended to be for students to experiment with.
The shapes of the graphs will change before their very eyes!
Having experimented with plastic blocks, and graphs, and/ or spreadsheets, your students should find that diagrams like these hold no horrors for them.